5

Most airlines board passengers starting from the back of the plane and then working their way towards the front (after boarding priority classes and passengers).

In an episode of Mythbusters, Adam and Jamie tested the myth that the boarding strategy favoured by most airlines, back to front, is the least efficient.

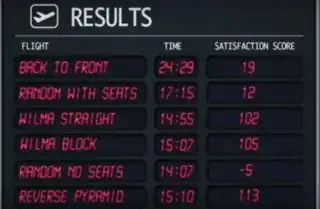
The myth was confirmed, and these were the results:

enter image description here

The random no seats strategy is the fastest, followed by the WILMA straight strategy. However, random no seats strategy gives the lowest satisfaction scores.

The highest satisfaction score is given by the reverse pyramid strategy even though it is the fourth fastest.

How might one determine the optimal boarding strategy based solely on times and satisfaction scores given (not including advanced stuff like computing expected aisle or seat interferences)?

I can't seem to think of any kind of unit conversion except to convert the time to seconds and then multiply it with satisfaction score so it's like we're trying to maximise the product of time and satisfaction score:

$$f(t,s) = ts$$

What are some of the advantages or disadvantages of doing this?

One disadvantage seems to be that ranking by product of time and satisfaction score gives the same ranking by satisfaction score.

What else could be done? All that seem to come to mind are products so perhaps I might maximise anything like these:

$$f(t,s) = t^2s$$

$$f(t,s) = ts^{1/2} \text{(eliminating random no seats)}$$

$$f(t,s) = t(s-s_{ave})$$

I'm thinking we're going to have to relate time and satisfaction score to some unit such as money. So, one would have to find some relationship (for example, a linear relationship through linear regression) between boarding time and cost and then another between satisfaction score for boarding today and revenue from flight next month?

Does it have to be something like that?

I was suggested z-score so I tried standardising or something:

enter image description here

Why did the sum of squares of z's turn out to be 6 for both? Did I do something wrong? Is that the fourth moment of standard normal or something?

amoeba
  • 93,463
  • 28
  • 275
  • 317
BCLC
  • 2,166
  • 2
  • 22
  • 47
  • See [Creating an index of quality from multiple variables to enable rank ordering](http://stats.stackexchange.com/q/9358/17230) & [NIST, *Engineering Statistics Handbook*, 5.5.3.2.2, "Multiple responses: The desirability approach"](http://www.itl.nist.gov/div898/handbook/pri/section5/pri5322.htm). And the sum of the squared z-scores is 6 because that's the denominator you used in your calculation of the standard deviation: $\sum\left(\frac{x-\bar{x}}{\sqrt{\sum{(x-\bar{x})^2/n}}}\right)^2=?$ But of course there's no necessary relation between z-scores & utility, as @Kodiologist points out. – Scortchi - Reinstate Monica May 13 '16 at 13:55

1 Answers1

1

Unfortunately, in an optimization scenario with multiple quantities to be optimized, there is no easy way out of deciding for oneself how to balance the quantities to be optimized against one another. Trying to convert time and satisfaction scores to money saved by the airline, and then optimizing by money saved, is probably the most reasonable of the possibilities you've mentioned. The other possibilities all seem to blindly assume that time and satisfaction score are already in comparable units (that is, that 1 second of time is of equal importance as 1 point of satisfaction; or in the case of z-scores, that 1 SD of one is equal to 1 SD of the other), which I see no reason to believe.

One possibility you haven't mentioned is to first choose a minimum or maximum acceptable value for one of the two criteria, and then optimize the other. For example, you could choose a minimum acceptable satisfaction score and then choose the fastest strategy that satisfies that minimum.

Besides all this, though, it sounds from your description that each strategy was tested only once. This suggests the estimates of time and satisfaction are extremely imprecise, in which case the whole exercise is kind of pointless without more data.

Kodiologist
  • 19,063
  • 2
  • 36
  • 68