Model fitting: resampling the validation set to obtain distributions of test statistic

Question

I see many descriptions of splitting the data set into a training part, a validation part and a test part. We train our models on the training part and choose the best model using the validation part, finally seeing how the best model performs on the test set. We choose the best model in the validation part using some kind of test statistic, say MSE. But what do we do when the MSE for say two models are really close? From the law of parsimony I might want to choose the most parsimonious model (of, say, two competing models) even though the MSE for the parsimonious model is a bit higher. I propose here a model selection method:

Algorithm would be like this:

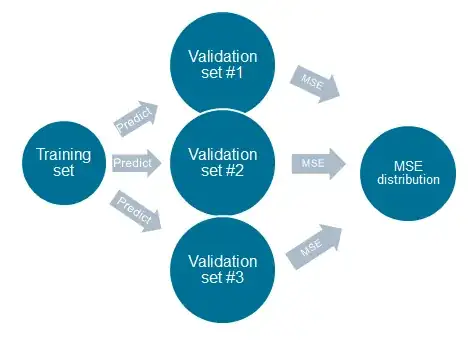
1) Train your models on the training set
2) Sample with replacement the validation set into K validation sets 
3) Predict using your models on each validation set
4) Calculate the MSE/MSPE for all the models on the K validation sets
4) Calculate the MSE/MSPE distributions from your K MSE/MSPE-calculations

In a scenario where the MSE/MSPE distributions of two competing models are more or less overlapping, I would choose the most parsimonious model. It would basically be a test of $H_0: \text{Predicative capabilities of parsimonious model equals complex model}$.

If the mean of $\text{MSE}_1$ is well within the 95th percentile of distribution of $\text{MSE}_2$, we choose the most parsimonious model of the two, regardless of which model has the lowest MSE.

Question: Does this method make sense to anybody else but me? Also, is this described anywhere else in the statistical litterature?

EDIT: It might seem like a similar question is asked here

Answer 1

Not having thought too hard about this, my first guess is that the mean MSE from your bootstrapping procedure, given enough replicates, would equal the plain old MSE for the validation set.

Stepping back, though, I don't see how the bootstrapping procedure would help with your original problem, "what do we do when the MSE for say two models are really close?" In that situation, you can pick the model that has the (however slightly) lower MSE, or the simpler model, or whatever you like, really. Since the MSE is very similar, the models should have very similar predictive performance, so it shouldn't matter so much which you pick. You can also hunt for other useful ways the models might differ, as in this paper (Arfer & Luhmann, 2015), where I tried shrinking the dataset and adding noise to see if some models were more robust than others.

Arfer, K. B., & Luhmann, C. C. (2015). The predictive accuracy of intertemporal-choice models. British Journal of Mathematical and Statistical Psychology, 68, 326–341. doi:10.1111/bmsp.12049

Answer 2

There are enough statistical tests to decide if one model preforms better than another model. In your case you want to know if the mean of the squared errors of one model is significantly better than the mean of the squared errors of another model (your H0 hypothesis). It makes sense to choose the simpler model if there is no significant difference (Ockham's razor).

You can test this hypothesis without bootstrapping because you know all the seperate error terms that make up the MSE. These seperate error terms are all independent estimates of the MSE. Bootstrapping is useful if you cannot use the population to get an confidence level of the estimate, for example with accuracy. But the variance of the MSE is well defined.

A common way is to describe the certainty of the MSE is the standard error (https://en.wikipedia.org/wiki/Standard_error):

$\text{SE}\ = \frac{s}{\sqrt{n}}$

This is basically the uncertainty of your MSE estimate. You can compute each MSE and look if the difference between the MSE's is higher than the sum of their standard errors to see how significant the difference is. But you can also use a t-test or ANOVA for this.