Why is the F-test for difference in variance so sensitive to the assumption of normal distribution, even for large $N$?
I have tried to search the web and visited the library, but none of it gave any good answers. It says that the test is very sensitive for violation of the assumption for normal distribution, but I do not understand why. Does anyone have a good answer for this?
I presume you mean the F-test for the ratio of variances when testing a pair of sample variances for equality (because that's the simplest one that's quite sensitive to normality; F-test for ANOVA is less sensitive)
If your samples are drawn from normal distributions, the sample variance has a scaled chi square distribution
Imagine that instead of data drawn from normal distributions, you had distribution that was heavier-tailed than normal. Then you'd get too many large variances relative to that scaled chi-square distribution, and the probability of the sample variance getting out into the far right tail is very responsive to the tails of the distribution from which the data were drawn=. (There will also be too many small variances, but the effect is a bit less pronounced)
Now if both samples are drawn from that heavier tailed distribution, the larger tail on the numerator will produce an excess of large F values and the larger tail on the denominator will produce an excess of small F values (and vice versa for the left tail)
Both of these effects will tend to lead to rejection in a two-tailed test, even though both samples have the same variance. This means that when the true distribution is heavier tailed than normal, actual significance levels tend to be higher than we want.
Conversely, drawing a sample from a lighter tailed distribution produces a distribution of sample variances that's got too short a tail -- variance values tend to be more "middling" than you get with data from normal distributions. Again, the impact is stronger in the far upper tail than the lower tail.
Now if both samples are drawn from that lighter-tailed distribution, the this results in an excess of F values near the median and too few in either tail (actual significance levels will be lower than desired).
These effects don't seem to necessarily reduce much with larger sample size; in some cases it seems to get worse.
By way of partial illustration, here are 10000 sample variances (for $n=10$) for normal, $t_5$ and uniform distributions, scaled to have the same mean as a $\chi^2_9$:
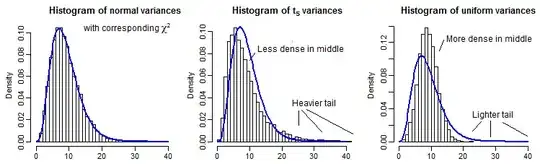
It's a bit hard to see the far tail since it's relatively small compared to the peak (and for the $t_5$ the observations in the tail extend out a fair way past where we have plotted to), but we can see something of the effect on the distribution on the variance. It's perhaps even more instructive to transform these by the inverse of the chi-square cdf,
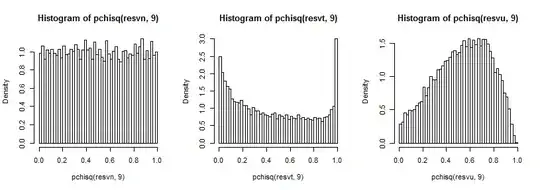
which in the normal case looks uniform (as it should), in the t-case has a big peak in the upper tail (and a smaller peak in the lower tail) and in the uniform case is more hill-like but with a broad peak around 0.6 to 0.8 and the extremes have much lower probability than they should if we were sampling from normal distributions.
These in turn produce the effects on the distribution of the ratio of variances I described before. Again, to improve our ability to see the effect on the tails (which can be hard to see), I've transformed by the inverse of the cdf (in this case for the $F_{9,9}$ distribution):
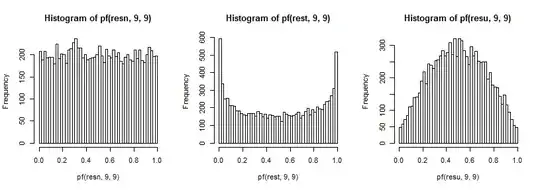
In a two-tailed test, we look at both tails of the F distribution; both tails are over-represented when drawing from the $t_5$ and both are under-represented when drawing from a uniform.
There would be many other cases to investigate for a full study, but this at least gives a sense of the kind and direction of effect, as well as how it arises.
As Glen_b has illustrated brilliantly in his simulations, the F-test for a ratio of variances is sensitive to the tails of the distribution. The reason for this is that the variance of a sample variance depends on the kurtosis parameter, and so the kurtosis of the underlying distribution has a strong effect on the distribution of the ratio of sample variances.
To deal with this issue, O'Neill (2014) derives a more general distributional approximation for ratios of variances that accounts for the kurtosis of the underlying distribution. In particular, if you have a population variance $S_N^2$ and sample variance $S_n^2$ with $n<N$ then Result 15 of that paper gives the distributional approximation$^\dagger$:
$$\frac{S_N^2}{S_n^2} \overset{\text{Approx}}{\sim} \frac{n-1}{N-1} + \frac{N-n}{N-1} \cdot F(DF_C, DF_n),$$
where the degrees-of-freedom (which depend on the underlying kurtosis $\kappa$) are:
$$DF_n = \frac{2n}{\kappa - (n-3)/(n-1)} \quad \quad \quad DF_C = \frac{2(N-n)}{2+(\kappa-3)(1-2/N+1/Nn)}.$$
In the special case of a mesokurtic distribution (e.g., the normal distribution) you have $\kappa=3$, which gives the standard degrees-of-freedom $DF_n = n-1$ and $DF_C = N-n$.
Although the distribution of the variance-ratio is sensitive to the underlying kurtosis, it is not actually very sensitive to normality per se. If you use a mesokurtic distribution with a different shape to the normal, you will find that the standard F-distribution approximation performs quite well. In practice the underlying kurtosis is unknown, so implementation of the above formula requires substitution of an estimator $\hat{\kappa}$. With such a substitution the approximation should perform reasonably well.
$^\dagger$ Note that this paper defines the population variance using Bessel's correction (for reasons stated in the paper, pp. 282-283). So the denominator of the population variance is $N-1$ in this analysis, not $N$. (This is actually a more helpful way to do things, since the population variance is then an unbiased estimator of the superopopulation variance parameter.)
