Verifying and/or changing priors assumptions on Bayesian ANOVA

Question

I am performing a Bayesian analysis of around 1500 data, divided into 2 factors, one that I am interested x1, and the id-variable for the paired/within-subject x2. x1 has 15 levels, and x2 around 100 subjects.

Basically, the hierarchical model is:

y[i] ~ dt(a_0 + b[x1[i]] + c[x2[i]] , sigma, df)  (1)
b[j] ~ dnorm( ... )      for all levels j of x1  (2)
c[k] ~ dnorm( ... )      for all levels k of x2  (3)
a_0 ~ dnorm( ... )                               
... plus the higher level models for the parameters in (2), (3) and sigma and df

using a JAGS-like language. x1[i] returns the x1 value of data i, b[x1[i]] is the deflection for that level of x1. I am using the model (and code) by John Kruschke at http://doingbayesiandataanalysis.blogspot.com/ which accompanies his book (the code is for the 2nd edition but I have only read the first edition so maybe my questions are answered in the 2nd edition?)

I have 3 questions, and I understand that having multiple questions on a single post may inhibit potential answerers, since one may know one answer but not all. I welcome partial or full answers to any one of my subquestions.

Q1) Should I use a beta distribution for the y, since my data is between 0 and 1?

Yes, all the y's are between 0 and 1, and they measure rates.

I think the answer here is NO, one should not use a beta distribution for line (1) of the model. a) First I could not find any papers/sites on priors for the beta. b) Second I see no good justification for having a beta at the first line of the model - the dt is a model of the prediction errors. How could a beta there be a model of errors?, It seems to be just a way to guarantee that the predictions are not outside the correct range.

So I am somewhat sure that the answer is NO.

Q2) Should I transform the data?

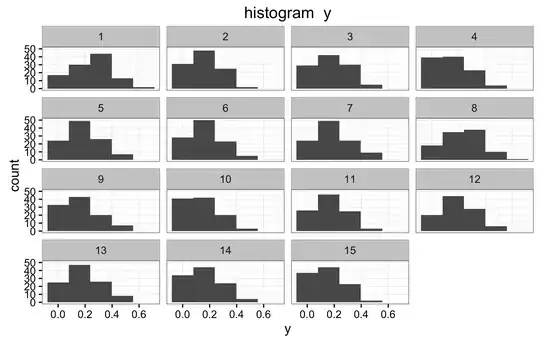
Below is the histogram of the all the y values. The histogram seems to be bimodal, which I believe makes things harder.

I read somewhere (I cannot find it where now) that one usual transformation for 0-1 data is to use the logit transform, so there are no longer limits to the y, and one does no longer have to worry about it. But in this case, I think the group of data with 0 value will cause me much more trouble than solutions brought by the logit.

The data us skewed to the left, but I don't think this in itself should be a problem. If the y's are log-normal distributed, then very likely the prediction errors are not normally or student-t distributed, and thus the log transformation. But in this case, all data is limited, and therefore the errors are not necessarily very large.

Anyway, I sqrt transformed the data, since it is easy to do. Below the histogram. But some of the analysis I am interested changed significantly with this transformation. For example, one of the contrast I am analyzing, went form 90% within the ROPE to 100% in the ROPE. I don't know if this is due to he fact that the prior distributions are better descriptions of the data, or because the ROPE is now larger (as is the data) since I am taking the sqrt of rates.

Q3) How do I verify if the priors in (2) and (3) are ok for the data, and if that are not, which new priors choose?

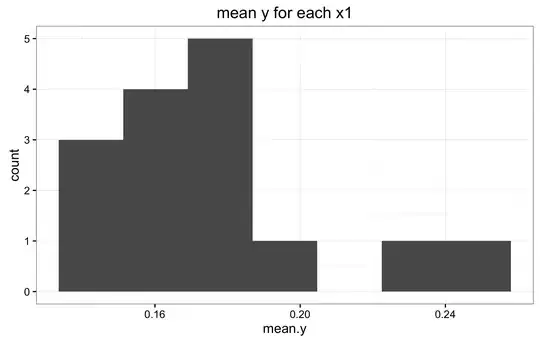
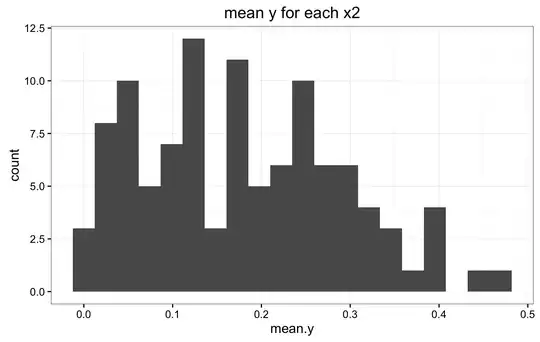
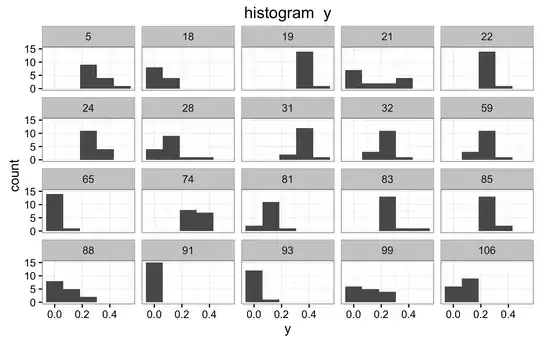
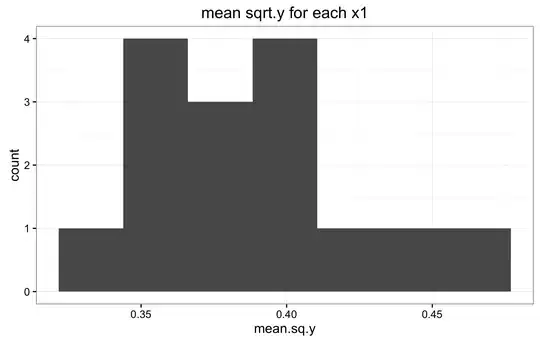
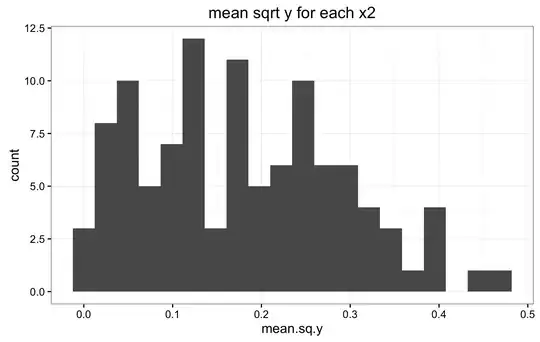
This is the difficult question for me. I am not sure, nor do I know how to verify if the priors in (2) and (3) are the correct ones. Below are the histograms of the mean y for all values X1, and the mean y for all values of X2. Also a panel of histograms of y for each x1, and a histograms for a random selection of subjects.I don't know how to interpret these histograms to verify if indeed (2) and (3) are appropriate priors. If they are not, is there any other suggestions?

Below are the two mean y histograms for the sqrt transformed data.

UPDATE 09/2016

The paper where I use the Bayesian ANOVA is published at ArXiv. The paper has some lengthy discussion on the suitability of the model for the problem (of comparing many classifiers on many data sets). I end up using the posterior predictive checking mentioned by @ssdecontrol to show that the Gaussian priors are not that bad.

I used a dnorm in equation (1) instead of the student-t (which was too forgiving)

I think the binomial model proposed by @C.R.Peterson looks promising and in time I will try it on that data.

Answer 1

Developing hierarchical models involves a fair amount of decision making from the modeler, so most of what I present here should be viewed as a recommendation, not as solid statistical fact.

Based on your comments above, your response rates are actually estimated from a number of success/failure trials. Estimating these error rates outside of the model is essentially equivalent to assuming that this is the true error rate with 100% certainty; for observations where you calculated a 0% error rate, you would essentially be saying that errors are impossible. Estimating these rates as part of the model would allow you to incorporate and account for that uncertainty.

In this response, I'm not going to address your three questions individually; Questions 1 and 2 are superseded by my suggestion that you use the the raw number of trails with and without errors instead of the proportion. The majority of this answer addresses prior selection.

First, here is the model I would use: $$\begin{align*} Y_{i} &\sim \mbox{Binomial}(N_{i},p_{i})\\ \mbox{logit}(p_{i}) &= \alpha_{j|i}+\beta_{k|i}\\ \alpha_{j} &\sim \mbox{Normal}(\mu,\sigma_{\alpha})\\ \mu_{i} &\sim \mbox{Normal}(0,2)\\ \sigma_{\alpha} &\sim \mbox{Cauchy}^{+}(0,1)\\ \beta_{k} &\sim \mbox{Normal}(0,\sigma_{\beta})\\ \sigma_{\beta} &\sim \mbox{Cauchy}^{+}(0,1)\end{align*}$$

For each of your 1500 data points, you have $N_{i}$ total trials, out of which $Y_{i}$ is the number of trials that did not contain an error.

$\alpha_{j}$ is the baseline intercept for subject $j$ (where the value for $j$ for any given $i$ is determined by your $x_{2}$ indicator). $\beta_{k}$ is the effect of treatment $k$ (likewise, the value of $k$ is determined by the $x_{1}$ indicator). This assumes that the effect of each treatment does not vary among subjects.

$\alpha_{j}$ is modeled hierarchically around $\mu$, which is the overall baseline log-odds of a trial not having an error (ignoring treatment and subject). Feel free to vary the standard deviation of its prior a bit; I chose 2 because the inverse $\mbox{logit}^{-1}(4)=.98$, meaning that 95% of the probability mass for the average of $p$ is between .02 and .98. $\sigma_{\alpha}$ controls the variation among each subject's baseline; Gelman (2006) recommends half-Cauchy priors for hierarchical scale parameters. A half Student-t prior with 3-7 degrees of freedom could also be appropriate, and would allow for greater shrinkage towards $\mu$. I would go with a scale parameter of 1 for this prior (because a shift of 1 in logit-space is rather large), but larger values would allow for greater variation.

While $\beta$ could be treated as a “fixed effect” (and many people would argue that that it should be), modeling them with a common prior for standard deviation would impose regularization that would help guard against multiple comparisons (Gelman et al., 2012). A half Cauchy-prior would again be appropriate in this case, since it would allow $\sigma_{\beta}$ to be very large (which would essentially turn it into a no-pooling/fixed effects model, with each $\beta_{k}$ estimated separately), or very small (which shrink each effect to 0, meaning no difference among treatments).

After running the model, you could estimate the overall error rate of each treatment as $\mbox{logit}^{-1}(\mu+\beta_{k})$.

I would also recommend using a posterior predictive check for your model (i.e., generating new data with your posterior distribution and checking it against your real data). This is a particularly effective way to check the adequacy of your model.

All of this is fairly easy to implement in Stan, and will almost certainly be faster than a JAGS implementation. Here is some sample Stan code:

data{
  int nObs;
  int N[nObs];
  int Y[nObs];
  int nSubject;
  int nTreatment;
  int<lower=1, upper=nTreatment> x1[nObs];
  int<lower=1, upper=nSubject> x2[nObs];
}
parameters{
  vector[nTreatment] alpha;
  real mu;
  vector[nSubject] beta;
  real<lower=0> sigma_alpha;
  real<lower=0> sigma_beta;
}
model{
  alpha ~ normal(mu, sigma_alpha);
  sigma_alpha ~ cauchy(0, 1);
  mu ~ normal(0,1);
  beta ~ normal(0,sigma_beta);
  sigma_beta ~ cauchy(0,1);
  Y ~ binomial_logit(N, alpha[x2] + beta[x1]);
}
generated quantities{ // This part of the model does not involve sampling
  vector[nTreatment] prob_treat; // This is the posterior probability of each treatment, accounting for variation within subjects
  vector[nTreatment] prob_Y; // This is the posterior probability of having no errors (i.e, your error rate)
  int yNew[nObs]; // New observations for a posterior predictive check
  for(i in 1:nTreatment)
    prob_treat[i] <- inv_logit(mu + beta[i]);
  // Posterior Predictive check
  for(i in 1:nObs){
    prob_Y[i] <- inv_logit(alpha[x2[i]]+beta[x1[i]])
    yNew[i] <- binomial_rng(N[i], prob_Y[i]);
  }
}

Answer 2

1. Yes, you should use a distribution that is designed to model the data you have. Don't think of dt as a model of prediction errors. It's your model of the distribution of your response variable conditional on the predictors. Your response is a rate. If you can model it with a beta distribution, you should model it with a beta distribution. Do beware the folk theorem propagated by Andrew Gelman: paraphrasing, it says that if your statistical computation is difficult, it is probably your model that needs to be revised. That said, statistical computation (and especially Bayesian statistical computation) is easier than ever with Stan, and issues like lack of conjugacy are no longer (by themselves) an obstacle. Beta regression in Stan is straightforward: see How can I model a proportion with BUGS/JAGS/STAN? for an appropriate parameterization that might set you at ease about priors.

2. If you are using the correct distribution to model your responses, no, you don't need to transform your responses. You do, however, need to transform your predictors. Your model will be numerically unstable when the variable scales differ dramatically, and even when they only differ by small amounts it is hard to separate differing effect sizes from differing predictor variances. I heard Gelman talk at the beginning of last month, and he said that normal(0, 1) was his "new favorite prior." He is a big proponent of parameterizing your model in such a way that your parameters are all on the same scale, and I believe this is very reasonablw advice.

3. If you read the above two points, hopefully you'll realize that it's not a big deal! But you absolutely can and should check the results of your entire model. Likely you will end up wanting to change something other than your priors.

Answer 3

Your first two questions sort of belong together. Firstly, for judging the need for a transformation to decide between, say, untransformed normal model, log-normal and square-root transformation, it is not really the right thing to look at the raw data, but rather at the model residuals. In this case it appears that the data is $\geq 0$ and possibly bounded to $[0,1]$ - you would presumably know whether this is the case (e.g. if these are proportions or some measurement that can only ever be in this interval). A beta distribution could in theory be an option that results in data that lies in $[0,1]$, but like a log-normal distribution or normal distribution for square-root transformed values one concern is that you say you have exactly zero for several observations. This should not happen with these distributions. If it is due to rounding or measurement precision, then you could build that into the model (with a likelihood contribution corresponding to the probability of the measurement falling below the minimum value that would count as non-zero).

Alternatively, if these values are in fact proportions, then some type of binomial model (taking into account known correlations - e.g. each observation is from one subject, so a random subject effect on the logit scale may make sense) would likely be the best choice, but you would need to know the number of binomial samples taken to get each proportion. Similarly, if these are rates, then count models (e.g. Poisson or negative binomial) would make sense.

Regarding your choice of priors: What do you want your priors to do? Include available prior information? Presumably that is not what you are trying to do, because you seem to have little prior knowledge on the problem. Stabilize inference a bit when data are sparse, but otherwise influence inference as little as possible? Induce shrinkage in order to avoid excessively easy evidence of effects? Each would result in different choices. The choice should not directly depend on the exact observed data, but only on the nature of the data, the scale of the data (or link function to ensure sensibly scaled priors for the effects, e.g. for a binomial model with a logit link a Cauchy(0, 2.5) prior has been proposed as a default prior), how the data was generated and what behaviour is desirable (e.g. you could make the predictors for each category shrink towards each other by having a random effect on the means of the priors).