Fit circle of fixed diameter over most dense area of scatterplot

Question

I am looking for a function that would help make a circle (of fixed diameter) over the most data points (highest density) on a two-dimensional scatter plot. I was hoping someone would at least point me in the direction I should be looking. I'm willing to do my own math. I was going to utilize this for a computer program.

Answer 1

Let's assume you have points ${\bf p_1, p_2, \ldots, p_k}\in\mathbb{R}^n$. Then your problem can of finding the $r$-diameter sphere containing the most points can be formulated as a mixed integer quadratically constrained program (MIQCP), with ${\bf x}\in\mathbb{R}^n$ as the center of the sphere and ${\bf y}\in\{0, 1\}^k$ defining whether each point is within $r$ distance of the center:

$$ \begin{array}{rl} \max & \sum_{i=1}^k y_i \\ \mathrm{subject~to} & \sum_{j=1}^n (x_j - p_{ij})^2~\leq~r^2+M(1-y_i)~~\forall~i \\ & y_1, y_2, \ldots, y_k~~\in~~\{0, 1\} \end{array} $$

Here, $M$ is an appropriately large constant. This can be formulated and solved by MIQCP-solving software, such as BARON, Couenne, or GAMS.

MIQCPs are difficult to solve, and the problem would be a good deal simpler to solve if you instead wanted to find the point that has Manhattan distance (aka 1-norm distance) of no more than $r$ from as many points as possible. This problem can be formulated as a mixed integer linear programming problem (MILP):

$$ \begin{array}{rl} \max & \sum_{i=1}^k y_i \\ \mathrm{subject~to} & \sum_{j=1}^n z_{ij}~\leq~r+M(1-y_i)~~\forall~i \\ & z_{ij}~\geq~x_j - p_{ij}~~\forall~i,~j \\ & z_{ij}~\geq~p_{ij} - x_j~~\forall~i,~j \\ & y_1, y_2, \ldots, y_k~~\in~~\{0, 1\} \end{array} $$

MILPs can be solved with many different solvers, including both open-source and commercial options (commercial options will be needed for large problem instances). For instance, here is an implementation using the lpSolve package in R, using 25 randomly generated points and (1-norm) distance 1:

library(lpSolve)
# P is a k x n matrix
get.center <- function(P, r) {
  n <- ncol(P)
  k <- nrow(P)
  ij <- apply(expand.grid(i=1:k, j=1:n), 1, paste, collapse=" ")
  vars <- rbind(data.frame(type="xp", i=NA, j=1:n),
                data.frame(type="xn", i=NA, j=1:n),
                data.frame(type="y", i=1:k, j=NA),
                data.frame(type="z", i=rep(1:k, each=n), j=rep(1:n, k)))
  ij <- vars[vars$type == "z",c("i", "j")]
  M <- sum(apply(P, 2, max)) - sum(apply(P, 2, min))
  mod <- lp(direction="max",
            objective.in=(vars$type == "y")*1,
            const.mat=rbind(t(sapply(1:k, function(i) {
              (vars$type == "z" & vars$i == i) +
                M*(vars$type == "y" & vars$i == i)
            })),
            t(apply(ij, 1, function(idx) {
              (vars$type == "z" & vars$i == idx[1] & vars$j == idx[2]) -
                (vars$type == "xp" & vars$j == idx[2]) +
                (vars$type == "xn" & vars$j == idx[2])
            })),
            t(apply(ij, 1, function(idx) {
              (vars$type == "z" & vars$i == idx[1] & vars$j == idx[2]) +
                (vars$type == "xp" & vars$j == idx[2]) -
                (vars$type == "xn" & vars$j == idx[2])
            }))),
            const.dir=rep(c("<=", ">="), c(k, 2*n*k)),
            const.rhs=c(rep(r+M, k), -as.vector(t(P)), as.vector(t(P))),
            binary.vec=which(vars$type == "y"))
  mod$solution[vars$type == "xp"] - mod$solution[vars$type == "xn"]
}

set.seed(144)
P <- matrix(rnorm(50), nrow=25)
ctr <- get.center(P, 1)
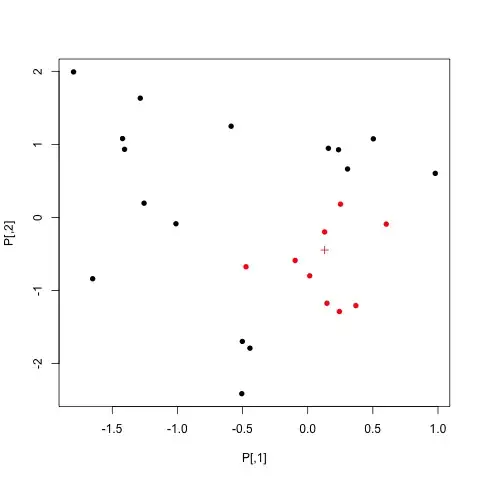
plot(P, pch=16, col=ifelse(abs(P[,1]-ctr[1]) + abs(P[,2]-ctr[2]) <= 1.00001, "red", "black"))
points(ctr[1], ctr[2], pch=3, col="red")

The red points are the points within 1-norm distance 1, and the plus is the selected center: