It has been said that ordinary least squares in y (OLS) is optimal in the class of linear unbiased estimators when the errors are homoscedastic and serially uncorrelated. Regarding homoscedastic residuals, the variance of the residuals is the same independent of where we would measure variation of residual magnitude on the x-axis. For example, suppose that the error of our measurement increases proportionately for increasing y-values. We could then take the logarithm of those y-values before performing regression. If that is done, the quality of fit increases compared to fitting a proportional error model without taking a logarithm. In general to obtain homoscedasticity, we might have to take the reciprocal of the y or x-axis data, the logarithm(s), the square or square root, or apply an exponential. An alternative to this is to use a weighting function, for example, to regress a proportional to y-value error problem, we may find that minimizing $\frac{(y-\text{model})^2}{y^2}$ works better than minimizing $(y-\text{model})^2$.
Having said that much, it frequently occurs that making the residuals more homoscedastic makes them more normally distributed, but frequently, the homoscedastic property is more important. That latter would depend on why we are performing the regression. For example, if the square root of the data is more normally distributed than taking the logarithm, but the error is proportional type, then t-testing of the logarithm will be useful for detecting a difference between populations or measurements, but for finding the expected value we should use the square root of the data, because only the square root of the data is a symmetric distribution for which the mean, mode and median are expected to be equal.
Moreover, it frequently occurs that we do not want an answer that gives us a least error predictor of the y-axis values, and those regressions can be heavily biased. For example, sometimes we might want to regress for least error in x. Or sometimes we desire to uncover the relationship between y and x, which is then not a routine regression problem. We might then use Theil, i.e., median slope, regression, as a simplest compromise between x and y least error regression. Or if we know what the variance of repeat measures is for both x and y, we could use Deming regression. Theil regression is better when we have far outliers, which do horrible things to ordinary regression results. And, for median slope regression, it matters little whether the residuals are normally distributed or not.
BTW, normality of residuals does not necessarily give us any useful linear regression information. For example, suppose we are doing repeat measurements of two independent measurements. Since we have independence, the expected correlation is zero, and the regression line slope can then be any random number with no useful slope. We do repeat measurements to establish an estimate of location, i.e., the mean (or median (Cauchy or Beta distribution with one peak) or most generally the expected value of a population), and from that to calculate a variance in x and a variance in y, which can then be used for Deming regression, or whatever. Moreover, the assumption that superposition therefore be normal at that same mean if the original population is normal leads us to no useful linear regression. To carry this further, suppose I then vary the initial parameters and establish a new measurement with different Monte Carlo x and y-value function generating locations and collate that data with the first run. Then the residuals are normal in the y-direction at every x-value, but, in the x-direction, the histogram will have two peaks, which does not agree with the OLS assumptions, and our slope and intercept will be biased because one does not have equal interval data on the x-axis. However, the regression of the collated data now has a definite slope and intercept, whereas it did not before. Moreover, because we are only really testing two points with repeat sampling, we cannot test for linearity. Indeed, the correlation coefficient will not be a reliable measurement for the same reason, it will suffer from the ordinary least squares (OLS) bias resulting from the assumption of no x-axis variance when there is a quite demonstrable x-axis variance.
Conversely, it is sometimes additionally assumed that the errors have normal distribution conditional on the regressors. This assumption is not needed for the validity of the OLS method, although certain additional finite-sample properties can be established in case when it does (especially in the area of hypotheses testing), see here. When then is OLS in y a correct regression? If, for example, we take measurements of stock prices at closing every day at precisely the same time, then there is no t-axis (Think x-axis) variance. However, the time of the last trade (settlement) would be randomly distributed, and the regression to discover the RELATIONSHIP between the variables would have to incorporate both variances. In that circumstance, OLS in y would only estimate the least error in y-value, which would be a poor choice for extrapolating trading price for a settlement, as the time itself of that settlement also needs to be predicted. Moreover, normally distributed error may be inferior to a Gamma Pricing Model.
What does that matter? Well, some stocks trade several times a minute and others do not trade every day or even every week, and it can make a rather big numerical difference. So it depends what information we desire. If we want to ask how the market will behave tomorrow at closing, that is an OLS "type" question, but, the answer may be nonlinear, non-normal residual and require a fit function having shape coefficients that agree with the derivatives fit (and/or higher moments) to establish the correct curvature for extrapolation. (One can fit derivatives as well as a function, for example using cubic splines, so the concept of derivative agreement should not come as a surprise, even though it is seldom explored.) If we want to know whether or not we will make money on a particular stock, then we do not use OLS, as the problem is then bivariate.
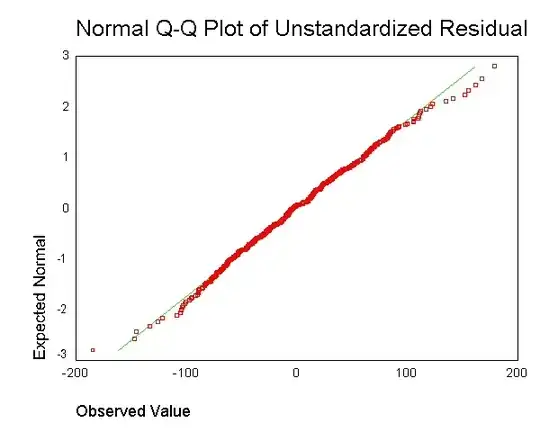 . However, I don't understand what the point is of obtaining the residual for each data point and mashing that together in a single plot.
. However, I don't understand what the point is of obtaining the residual for each data point and mashing that together in a single plot.