Negative Binomial to Normal

Question

I want to use normalisation technique that has assumption of residuals' normality (GLMs), but my data is $\sim$Negative Binomial.

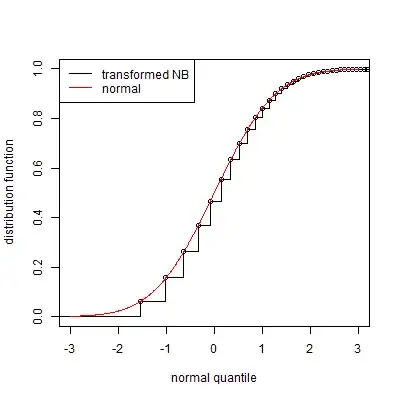
Can I map values from NB distributed distribution to Normal distribution, using probabilities and cumulative distribution function? I.e., I have a point $a$ and NB CDF says that 45% of points are less than $a$, can I map it to the point with the same property in Normal, apply normalisation and then apply reverse transformation to normalised data?

Switch to NB GLM is not feasible (the normalisation technique is really complicated, but effective, so it is not possible to quickly modify it for NB case). Authors of normalisation procedure recommend just to use variance-stabilization transformation (such as log or Anscombe), but I am not sure if it will be enough.

UPD: Data is experimental and there are a lot of data points. Bad data points (with small $mu$ and large variance, that can create problems for left tail) can be removed. What I really want to be able to do after this transformation: 1) remove batch effects using PCA or similar methods, 2) compare datapoints between samples.

UPD about PEER: this is the paper. The important thing is an equation 1). Let me explain. For each datapoint in sample $i$ and row $j$ I have a whole number $x_{ij}$ from $NB$ distribution. I need to transform $NB$-distributed data with the function $f$ to the data that can be modelled as: $RV(f(x_{ij})| conditions) \sim \mathcal N(different\_noise|conditions)$. So I need to find mapping from $NB$ distribution to somehow normal (with additional noise, etc).

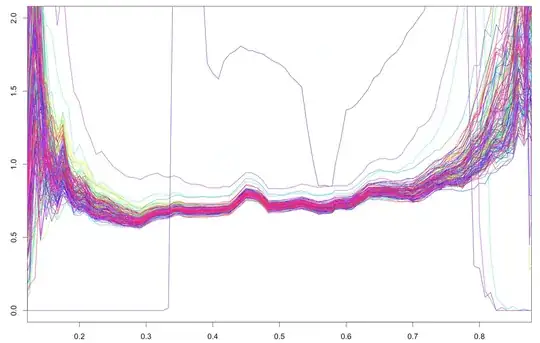
UPD about different variances across the samples: on $x$-axis is GC content, on $y$-axis: robust standard deviation of logarithms across all fragments with specified GC content, different plots - different samples.

Answer 1

A negative binomial random variable is discrete, so can't be transformed exactly into a continuous normal distribution.

For example, with a Bernoulli probability of 0.25 & counting the no. "failures" before the observation of 2 "successes", using your transformation gives

The approximation's especially bad in the lower tail—nought isn't a very improbable outcome, but negative counts are impossible

Answer 2

In theory one of the variance-stabilizing approaches should be sufficient, but this is contingent mainly on sample size. For small sample sizes this approach is problematic.

I am presuming that you have RNA-seq data that you would like to transform to use the PEER approach. Bear in mind that the methods developed in the paper you cite are meant for microarray data, where the normality assumption may be satisfied and sample sizes are large, assumptions that are usually violated in most RNAseq studies.

If you have a large enough sample size (approx > 30) I would suggest using the standard variance-stabilizing transformations such as the Anscombe transform.

If your sample sizes are small you could try the VST approach in the DESeq2 R package. Bear in mind that the vst modifies the mean expression values for the genes. After working through the math my take on it is that it a non-linear transformation wherefore it would not be appropriate for DE comparisons and perhaps the authors will comment on this ( presumably @whuber).

One other approach that I can think of which will definitely avoid the skewness issue is the so-called "Inverse Normal transform" see my post/thread here. From my understanding this will be alright to use when you are considering data from only a single class ( such as controls only) as they have applied for the networks analysis ( where i originally found the method). The statistical properties are a bit unclear, as in the posted link to a paper on that thread, and I am not quite sure how it would work when you want to make comparisons across classes as in a Differential Expression Analysis scenario.