A hair dresser's conundrum

Question

My hairdresser Stacey always puts on a happy face, but is often stressed about managing her time. Today Stacey was overdue for my appointment and very apologetic. While getting my haircut I wondered: How long should her standard appointments be? (if the customer's preference for clean round numbers could be ignored, for a moment).

Something to consider is a certain 'ripple effect' where one very late customer can lead to a string of delayed appointments. In reality, hair-dressers intuitively learn to space appointments longer and longer as they fear of these stressful days. But an optimum, elegant solution must be achievable by some statistical genius out there.. (if we dumb down reality a little)

Let's assume

a) hair cutting times are normally distributed and

b) there's only one hair dresser.

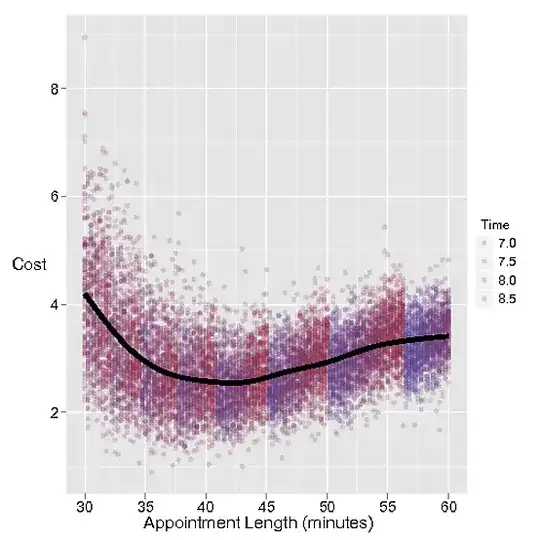
The cost of setting appointments too long is obviously the hairdresser's time wasted waiting for the next appointment. Let's cost this wasted time $1 per minute.

But if the appointment's not long enough, the next customer is kept waiting, which is a heavier cost of $3 per minute to customer-loving Stacey.

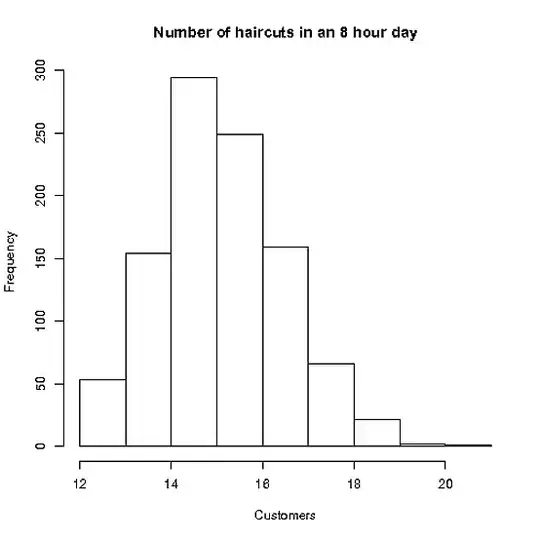
Stacey works up to 8 hours per day, and has enough demand that she can fill as many appointments as she can fit in
The mean hair cut takes her 30 minutes, with a std. dev of 10 minutes. (let's also assume men's cuts and women's cuts are the same!)

EDIT - some have rightly pointed out that Stacey could attend to EARLY customers ahead of their appointed time. This adds another layer of complexity, but if we treat this as quite a realistic problem we need to include it. Let's forget my 90/10 assumption and try for an assumption perhaps a little closer to reality.

Some customers are late and some are early. The mean of customers are 2 minutes late with a standard deviation of 2 minutes (sounds reasonably near reality no?)

Exactly how long should her appointments be?

@alexplanation sorry I've moved the goal posts on you! I'm sure R readers appreciate your answer.

if she has the ability to start the next haircut earlier than scheduled, she is not allowed to do so? — assumednormal, Jan 06 '12 at 06:41
As a rule of thumb Stacey should take arround 16 appointments... let’s start with this value: 16 appointments. Considering your model, the total time spent cutting hairs is a $\mathcal N( \mu = 8 \text{ hours}, \sigma = 40 \text{ minutes} )$. So at the end of the day she can easily be more than 30 minutes late, ie a shift by one appointment. Maybe the modeling is a bit unrealistic? Haircuts can be sped up a little bit when you are late... I don’t know anything on queuing theory. I think this is the kind of problem they address... — Elvis, Jan 06 '12 at 08:33
You are missing a couple of piece of information. 1) the distribution of early times OR the fact that early customers don't inflict any cost on Stacy until their scheduled appointment time, and 2) The distribution of late times. Maybe you should just specify a distribution of arrival times relative to the scheduled arrival time? — jbowman, Jan 06 '12 at 14:43
Also, what happens at the end of eight hours if she's not done with an appointment? If she continues working, clearly the last appointment should be scheduled for 8 hours after the first (which would be at the start of the day), regardless of how many appointments are scheduled. — jbowman, Jan 06 '12 at 16:55

alexplanation · Accepted Answer · 2012-01-06T19:45:17.103

There are a lot of moving parts in this problem, which makes it ripe for simulation.

First off, as Elvis mentioned in the comments, it seems like Stacey should take about 16 appointments, as each one is about half an hour. But you know that as the appointments start to get delayed, things start shifting later and later - so if Stacey is going to only start an appointment if she has half an hour left (so much for sweeping the hair off the floor, eh, Stacey?) then we're going to have less than 16 possible slots, if we used a crystal ball to schedule appointments with no resting time.

Optimally spaced haircuts

In the next simulation, we can investigate the curve of cost as a function of appointment length. Of course, the rest of the parameters will also end up playing a role here - and in reality, Stacey isn't going to schedule her appointments fractional minutes apart, but this gives us some intuition about what's going on.

enter image description here

I've also plotted the time that Stacey has to be at work as the color. I decided that Stacey would never schedule her last appointment after 7:30, but sometimes the appointment shows up late, or there's been a delay! You can see that the time she gets to go home is quantized, so that as appointments get longer, you get one less appointment and then don't have to work as late. And I think that's a missing element here - maybe scheduling your appointments 45 minutes apart is great, but you'll get an extra appointment in if you can squeeze it to 40. That cost is incorporated by Stacey's waiting (which is why the cost goes up as the appointment length goes up) but your valuation of Stacey's time waiting might not be correct.

Anyway, fun problem! And a good way to learn some ggplot goodness and remember that my R syntax is super shaky. :)

My code is below - please feel free to offer suggestions for improvement.

To generate the code for the top plot:

hairtime = 30
hairsd = 10

nSim = 1000
allCuts = rep(0,nSim)
allTime = rep(0,nSim)

for (i in 1:nSim) {
    t = 0
    ncuts = 0

    while (t < 7.5) {
        ncuts = ncuts+1
        nexthairtime = rnorm(1,hairtime,hairsd)
        t = t+(nexthairtime/60)
    }
    allCuts[i] = ncuts
    allTime[i] = t
}

hist(allCuts,main="Number of haircuts in an 8 hour day",xlab="Customers")

The second simulation is a lot longer...

nSim = 100
allCuts = rep(0,nSim)
allTime = rep(0,nSim)

allCost = rep(0,nSim)

lateMean = 10
lateSD = 3

staceyWasted = 1
customerWasted = 3

allLengths = seq(30,60,0.25)

# Keep everything in 'long form' just to make our plotting lives easier later
allApptCosts = data.frame(matrix(ncol=3,nrow=length(allLengths)*nSim))
names(allApptCosts) <- c("Appt.Length","Cost","Time")
ind = 1

# for every appointment length...
for (a in 1:length(allLengths)) {
    apptlen = allLengths[a]
    # ...simulate the time, and the cost of cutting hair.
    for (i in 1:nSim) {
        appts = seq(from=0,to=(8-hairtime/60),by=apptlen/60)
        t = 0
        cost = 0
        ncuts = 0

        for (a in 1:length(appts)) {
            customerArrival = appts[a]
            # late!            
            if (runif(1)>0.9) {
                customerArrival = appts[a]+rnorm(1,lateMean,lateSD)/60
            }

            waitTime = t-customerArrival
            # negative waitTime means the customer arrives late
            cost = cost+max(waitTime,0)*customerWasted+abs(min(waitTime,0))*staceyWasted
                                        # get the haircut
            nexthairtime = rnorm(1,hairtime,hairsd)
            t = customerArrival+(nexthairtime/60)
        }
        allCost[i] = cost
        allApptCosts[ind,1] = apptlen
        allApptCosts[ind,2] = cost
        allApptCosts[ind,3] = t
        ind = ind+1
    }
}

qplot(Appt.Length,Cost,geom=c("point"),alpha=I(0.75),color=Time,data=allApptCosts,xlab="Appointment Length (minutes)",ylab="Cost")+
      geom_smooth(color="black",size=2)+
    opts(axis.title.x=theme_text(size=16))+
    opts(axis.title.y=theme_text(size=16))+
    opts(axis.text.x=theme_text(size=14))+
    opts(axis.text.y=theme_text(size=14))+
    opts(legend.text=theme_text(size=12))+
    opts(legend.title=theme_text(size=12,hjust=-.2))

Nice! Do you object showing the code? – Elvis Jan 06 '12 at 18:33 — Elvis, Jan 06 '12 at 18:33

A hair dresser's conundrum

1 Answers1