Convexity of linear regression

Question

I know that linear regression leads to a convex optimization problem. I'd like to visually show this with a simple example. Assume that there are two parameters (x and y) and a single data point <1, 1> with 2 as the y value (no intercept term. Then the cost function becomes

$$ (x+y-2)^2 $$

However if you plot this function you will get the figure 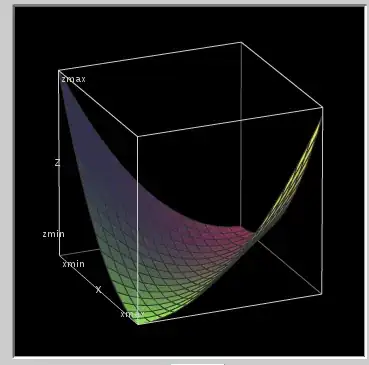which contains more than one minimal point. Where is the problem in this example? Thanks

Sycorax · Accepted Answer · 2016-04-07T18:57:56.480

6

2 parameters and a single data point is not strictly convex because the rank of the matrix of observations and predictors is deficient. Indeed, as you observe, there is a line of many "equally good" solutions, and this is because for any choice of $x$ there is a corresponding $y$ which achieves the minimum: how many points satisfy $x+y=2$?

Add more observations than predictors and the problem is (strictly) convex.

edited Apr 07 '16 at 18:57

answered Apr 07 '16 at 18:45

Sycorax

76,417
20
189
313

3

2 parameters and a single data point is convex, but not strictly convex, and the global minimum is not unique. It is not "not convex". – Mark L. Stone Apr 07 '16 at 18:53
@MarkL.Stone Yes, thanks, it always trips me up when "X" and "not X" don't quite exactly behave the way I might expect. – Sycorax Apr 07 '16 at 18:57
"more observations than predictors" exactly, thanks – Sanyo Mn Apr 07 '16 at 20:33
i.e., it is weakly convex – MichaelChirico Apr 08 '16 at 01:36

score 6 · Answer 2 · answered Apr 07 '16 at 18:49

6

$$(x+y-2)^2=0$$ $$x+y=2$$ $$y=2-x$$

You can pick any $x$, and get a corresponding $y$, i.e. there's no unique solution. With two unknowns and one observation, there's not going to be a unique solution

answered Apr 07 '16 at 18:49

Aksakal

55,939
5
90
176

Convexity of linear regression

2 Answers2

Linked