How can this time series be stationary?

Question

I have the following irregularly spaced time series.

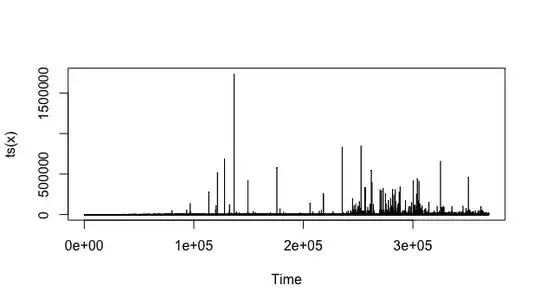
The related autocorrelogram is:

and I run the following tests:

> adf.test(x)

Augmented Dickey-Fuller Test

data:  x
Dickey-Fuller = -70, Lag order = 70, p-value = 0.01
alternative hypothesis: stationary

Warning message:
In adf.test(x) : p-value smaller than printed p-value


> kpss.test(x)

KPSS Test for Level Stationarity

data:  x
KPSS Level = 30, Truncation lag parameter = 100, p-value = 0.01

Warning message:
In kpss.test(x) : p-value smaller than printed p-value


> Box.test(x, type = "Ljung-Box")

Box-Ljung test

data:  x
X-squared = 20000, df = 1, p-value <2e-16

How can this time series be stationary? I suppose problems arise because my time series is irregularly spaced. In this case, there exist methods to assess stationarity with irregularly spaced time series?

See for instance https://domino.research.ibm.com/library/cyberdig.nsf/papers/E84BB1D4E1D2A8E48525706900694328/$File/rc23702.pdf as a start — kjetil b halvorsen, Jul 23 '19 at 22:32

Richard Hardy · Accepted Answer · 2016-04-05T10:31:59.010

2

While the data does not appear to have a unit root (which is also confirmed by the ADF test results), KPSS test rejects stationarity. Recall that the null hypothesis of KPSS is stationarity (in contrary to the ADF test). That is quite intuitive when you look at the graph.

Edit (to respond to edited post)
Of course, irregular spacing will be a problem. My answer only addresses the apparently incorrect interpretation of the KPSS test results.

edited Apr 05 '16 at 10:31

answered Apr 05 '16 at 10:30

Richard Hardy

54,375
10
95
219

Whoaaa ok! I wasn't aware that the null hypothesis of KPSS is stationarity! That makes sense! – stochazesthai Apr 05 '16 at 10:31
Are these tests somewhat robust against the extreme outliers and the extremely skewed distribution shown in the first figure? – Michael M Apr 05 '16 at 12:28
@MichaelM, Sorry, I don't know the answer. – Richard Hardy Apr 05 '16 at 13:12
1

@MichaelM, outliers will bias the ADF test towards rejecting the null of a unit root. The intuition is that the series will seem more mean reverting. – Plissken Apr 05 '16 at 17:16
Thank you@Plissken. The series looks like count data, so probably the test for stationarity is the least problem here. – Michael M Apr 05 '16 at 17:55

How can this time series be stationary?

1 Answers1