I would like some help in interpreting some odd cross-price elasticities that I got from my model. I estimated the following multinomial probit model and calculated the elasticities post-estimation:
$Alt_{i}=\beta_0 + \beta_1PriceA_i+\beta_2PriceB_{i}+\beta_3PriceC_{i}+\beta_4PriceD_{i}+ X\beta + \epsilon_i$
where $Alt_{i}$ is the type of health facility chosen by the individual decision-maker to have a one-time medical procedure (e.g. sterilization, medical circumcision, etc.) done. $Alt_{i}$ is a discrete choice variable with 4 levels, A, B, C, and D. The base outcome is facility type A.
The cross-price elasticities are shown in the table below. Non-significant elasticities are omitted from this table to make the output cleaner: $$\begin{array}{|c|c|c|c|} \hline & \text{A} & \text{B} & \text{C} & \text{D}\\ \hline \text{PriceA} & -0.34*& 0.15* & -0.35** & 0.16** \\ \hline \text{PriceB} & & & & \\ \hline \text{PriceC} & 0.13** & 0.13*** & -0.19** & -0.10* \\ \hline \text{PriceD} & -0.43** & &0.23* & 0.15* \\ \hline \end{array}$$ Note: * p<0.05; ** p<0.01; *** p<0.001
I am most interested in the interpretation of the effect of $PriceC$ on the probability of choosing Alternative D. Standard economic interpretation for a negative cross-price elasticity is that the two alternatives are complements, that is: an increase in the price of one alternative would result in a decrease in the predicted probability of choosing the other alternative. However, standard economic interpretation does not make sense in this case, because the two alternatives are not likely to be complements, because the procedure (e.g. sterilization) can only be done once.
I also noticed that an increase in $PriceD$ caused increases in the probability of using both facilities C and D. I can make an argument that an increase in the price of D would lead decision-makers to choose a lower-priced alternative (in this case, C), but what about the positive own-elasticity of D? My gut feeling is that there are other issues affecting preference, such as quality, not accounted for in the main model (I don't have measures of quality in my dataset). For example, service at Facility D is more expensive, but it may also be of higher quality, or at least perceived to be higher quality and preferred by the decision-maker (but if that's the case, then why is the cross-price elasticity of D with facility C positive?).
I was thinking about offering the following explanations, but I am not sure whether they explain the observed results fully:
This model should probably have been fitted as a nested logit model, since some of the alternatives may be nested. Of the 26 possible nesting combinations, the following 6 are plausible for this outcome alternative:
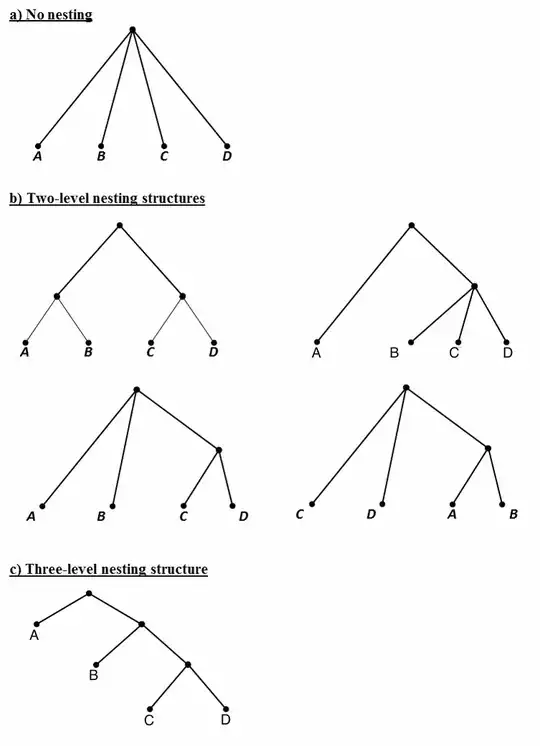
Could nested choice probabilities of the alternatives lead to the empirical results shown here?
Quality of care at facilities C and D may affect preference, but I don't have the variables for quality of care in my dataset, so the seemingly counterintuitive results may have stemmed from omitted variable bias.
Could anyone suggest other reasons for the results that I show here?