0

I am working on some stock analysis that I picked up to help me learn more about modeling.

I have become comfortable analyzing these plots when they are more as expected but I can't figure out why these are so wacky. I imagine there must be an explanation for these odd plots. Let me know if you have any idea how to analyze these.

plots of my lm model lm("Binary does next day go up or not" ~ predictor1 + predictor2 + predictor1*predictor2)

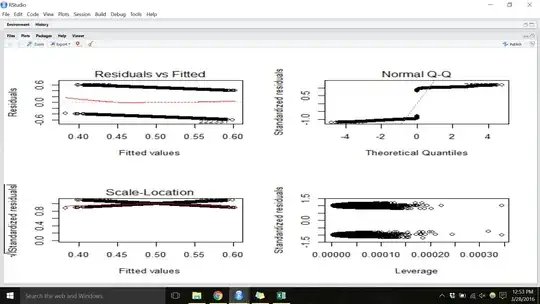
enter image description here

bpheazye
  • 3
  • 1
user110152
  • 1
  • 1
  • 4
    Your question is practically the same as the one at http://stats.stackexchange.com/questions/25068 . The resolution is a little different: `lm` is a least-squares model, which is inappropriate for these data. Your diagnostic plots make that abundantly clear. The fix is to use logistic regression. – whuber Mar 28 '16 at 18:28
  • Please register &/or merge your accounts (you can find information on how to do this in the **My Account** section of our [help]), then you will be able to edit & comment on your own question. – Silverfish Mar 28 '16 at 18:51

2 Answers2

3

Start from the definition, residual $=$ observed $-$ fitted, from which it immediately follows for any observed response that can be 0 or 1 that the residuals must fall on one of two lines,

residual $= 0 -$ fitted

residual $= 1 -$ fitted.

These lines are not horizontal, which would imply a band of identical residuals.

That explains the top-left plot. The top-right plot follows from noticing that you have two big clumps of residuals, one positive, one negative. Checking such residuals for normality is inappropriate any way. Normal errors aren't a plausible assumption here.

The other plots are easier to think about when you focus on this basic fact.

The bigger deal here is that regression sounds inappropriate for these data. You're reducing change to a binary outcome, which is your decision, but even then something like a logit regression would seem a better bet, as @whuber also comments.

The word incorrect in your title is therefore itself quite incorrect. Puzzling to you, indeed; inappropriate or unhelpful, arguably.

EDIT: The wording has been changed from incorrect to bad, which in my view is no better.

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
1

In logistic regression, as with linear regression, the residuals can be defined as observed minus expected values. The data are discrete and so are the residuals. As a result, plots of raw residuals from logistic regression are generally not useful. The binned residuals plot instead, after dividing the data into categories (bins) based on their fitted values, plots the average residual versus the average fitted value for each bin.

binnedplot(fitted(model_name), residuals(model_name, type = "response"), nclass = NULL, xlab = "Expected Values", ylab = "Average residual", main = "Binned residual plot", cex.pts = 0.8, col.pts = 1, col.int = "gray")

you can find more information, on this paper: http://vulstats.ucsd.edu/pdf/Gelman.ch-05.logistic-regression.pdf

erika vargas
  • 11
  • 1
  • Thank you for these interesting thoughts. It might help readers to know that the sense in which Gelman uses "discrete" here is unusual: the residuals themselves are decidedly *not* discrete. The residuals *for a given combination of explanatory values* will be discrete, but collectively they are not. – whuber Jun 13 '19 at 21:35