Does the assumption of Normal errors imply that Y is also Normal?

Question

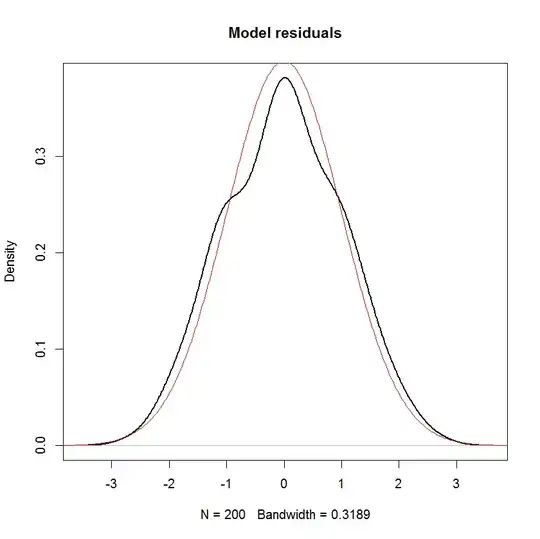
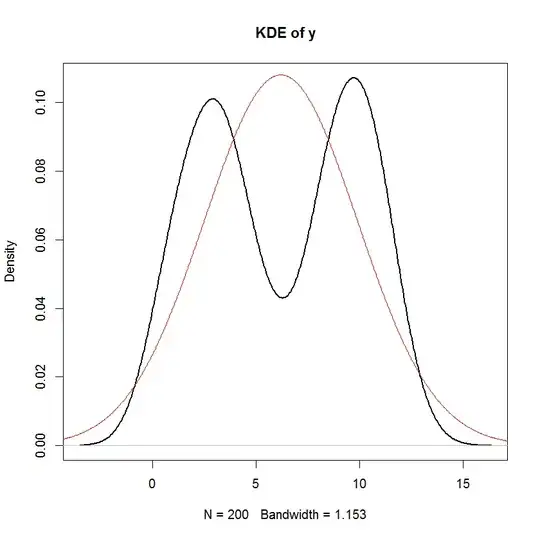
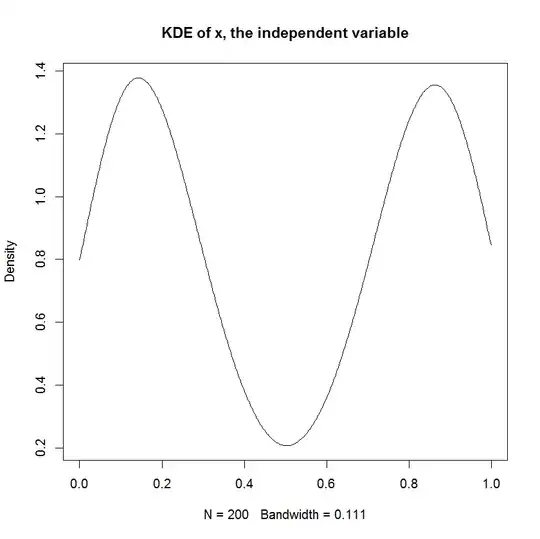
Unless I'm mistaken, in a linear model, the distribution of the response is assumed to have a systematic component and a random component. The error term captures the random component. Therefore, if we assume that the error term is Normally distributed, doesn't that imply that the response is also Normally distributed? I think it does, but then statements such as the one below seem rather confusing:

And you can see clearly that the only assumption of "normality" in this model is that the residuals (or "errors" $\epsilon_i$) should be normally distributed. There is no assumption about the distribution of the predictor $x_i$ or the response variable $y_i$.

Source: Predictors, responses and residuals: What really needs to be normally distributed?

Answer 1

The standard OLS model is $Y = X \beta + \varepsilon$ with $\varepsilon \sim \mathcal N(\vec 0, \sigma^2 I_n)$ for a fixed $X \in \mathbb R^{n \times p}$.

This does indeed mean that $Y|\{X, \beta, \sigma^2\} \sim \mathcal N(X\beta, \sigma^2 I_n)$, although this is a consequence of our assumption on the distribution of $\varepsilon$, rather than actually being the assumption. Also keep in mind that I'm talking about the conditional distribution of $Y$, not the marginal distribution of $Y$. I'm focusing on the conditional distribution because I think that's what you're really asking about.

I think the part that is confusing is that this doesn't mean that a histogram of $Y$ will look normal. We are saying that the entire vector $Y$ is a single draw from a multivariate normal distribution where each element has a potentially different mean $E(Y_i|X_i) = X_i^T\beta$. This is not the same as being an iid normal sample. The errors $\varepsilon$ actually are an iid sample so a histogram of them would look normal (and that's why we do a QQ plot of the residuals, not the response).

Here's an example: suppose we are measuring height $H$ for a sample of 6th graders and 12th graders. Our model is $H_i = \beta_0 + \beta_1I(\text{12th grader}) + \varepsilon_i$ with $\varepsilon_i \sim \ \text{iid} \ \mathcal N(0, \sigma^2)$. If we look at a histogram of the $H_i$ we'll probably see a bimodal distribution, with one peak for 6th graders and one peak for 12th graders, but that doesn't represent a violation of our assumptions.

Answer 2

Therefore, if we assume that the error term is Normally distributed, doesn't that imply that the response is also Normally distributed?

Not even remotely. The way I remember this is that the residuals are normal conditional on the deterministic portion of the model. Here's a demonstration of what that looks like in practice.

I start by randomly generating some data. Then I define an outcome which is a linear function of the predictors and estimate a model.

N <- 100

x1 <- rbeta(N, shape1=2, shape2=10)
x2 <- rbeta(N, shape1=10, shape2=2)

x <- c(x1,x2)
plot(density(x, from=0, to=1))

y <- 1+10*x+rnorm(2*N, sd=1)

model<-lm(y~x)

Let's take a look at what these residuals look like. I suspect that they should be normally distributed, since the outcome y had iid normal noise added to it. And indeed that is the case.

plot(density(model$residuals), main="Model residuals", lwd=2)
s <- seq(-5,20, len=1000)
lines(s, dnorm(s), col="red")

plot(density(y), main="KDE of y", lwd=2)
lines(s, dnorm(s, mean=mean(y), sd=sd(y)), col="red")

Checking the distribution of y, however, we can see that it's definitely not normal! I've overlaid the density function with the same mean and variance as y, but it's obviously a terrible fit!

The reason that this happened in this case is that the input data is not even remotely normal. Nothing about this regression model requires normality except in the residuals -- not in the independent variable, and not in the dependent variable.

Answer 3

No, it doesn't. For example, suppose we have a model predicting the weight of Olympic athletes. While weight could well be normally distributed among athletes in each sport, it won't be among all athletes - it might not even be unimodal.