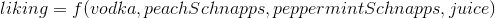I'm trying to find the optimal blend of 4 ingredients, to maximize liking of a beverage.
I can write a function for liking such as:
Liking is on a scale of 0 - 1 (0% - 100%).
I conducted 10 taste tests to gather data, then estimated a simple regression (this is in R):
# Data on blends tested in taste tests
X <- rbind( c(.93, .01, 0.03, .03 ),
c(.92, .02, 0.03, .03 ),
c(.94, .00, 0.03, .03 ),
c(.94, .02, 0.02, .02 ),
c(.91, .03, 0.03, .03 ),
c(.97, .01, 0.01, .01 ),
c(1, .00, 0.00, .00 ),
c(.92, .01, 0.03, .04 ),
c(1, .00, 0.00, .00 ),
c(.87, .05, 0.04, .04 )
)
# Liking results from taste tests
Y <- c(0.841217,
0.841213,
0.84121,
0.84121,
0.841204,
0.841201,
0.8412,
0.841187,
0.841187,
0.841172)
# Regression analysis (no intercept model)
glm(Y~X-1)
The results of the regression analysis were:
Call: glm(formula = Y ~ X - 1)
Coefficients:
X1 X2 X3 X4
0.8412 0.8404 0.8445 0.8386
Degrees of Freedom: 10 Total (i.e. Null); 6 Residual
Null Deviance: 7.076
Residual Deviance: 8.169e-10 AIC: -193.9
So, this gives me some insight as to the relative weight of each ingredient in determining liking, but it doesn't directly tell me which levels of the ingredients I should set to maximize liking. Of course, I could specify this model differently, such as using the binomial distribution or testing interactions, or worry about my small sample size, but I'm trying to keep it simple for now and focus on finding the right methodological framework for what I'm trying to do.
I was thinking that I could set up some sort of optimization function to determine the best levels (ingredient proportions) based on:
- The weights from the regression
- The constraint that the sum of the ingredients' proportions adds up to 1 (i.e. 100%)
- An objective function that specifies maximization of liking
- A constraint that liking is between 0 and 1
However, it's not clear to me how I can setup such an optimization model.
Am I heading in a reasonable direction? Is optimization the appropriate tool and, if so, how can such an optimization be setup (mapping the examples I found in various optimization packages to this use case was a point of confusion for me)?
Or, is it possible to determine the optimal levels directly from the regression results?