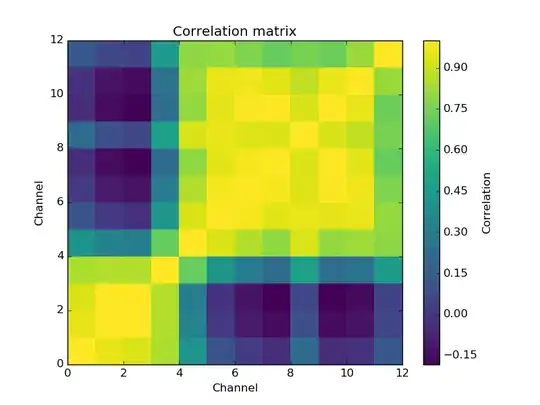
I am trying to predict a single response from twelve explanatory variables. There exist strong correlations between my variables. The correlation matrix looks as follows,
and the data have a condition number of 8889.9336. Therefore, I should expect that ordinary linear regression yields suboptimal results. However, it appears to perform rather well:
In [121]: reg = sklearn.linear_model.base.LinearRegression(fit_intercept=True)
In [122]: reg.fit(x[::2, :], y[::2])
Out[122]: LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
In [123]: reg.score(x[1::2, :], y[1::2])
Out[123]: 0.99986449992297743
In [124]: print((sqrt((reg.predict(x[1::2, :]).squeeze() - y[1::2])**2).mean()))
0.104017556147
When I use PLS1 including all components, performance is essentially identical to linear regression:
In [130]: reg2 = sklearn.cross_decomposition.PLSRegression(n_components=12, scale=False)
In [131]: reg2.fit(x[::2, :], y[::2])
Out[131]:
PLSRegression(copy=True, max_iter=500, n_components=12, scale=False,
tol=1e-06)
In [132]: reg2.score(x[1::2, :], y[1::2])
Out[132]: 0.99986450223986301
In [133]: print((sqrt((reg2.predict(x[1::2, :]).squeeze() - y[1::2])**2).mean()))
0.104024883567
and when I use less components, performance becomes worse:
In [134]: reg3 = sklearn.cross_decomposition.PLSRegression(n_components=9, scale=False)
In [136]: reg3.fit(x[::2, :], y[::2])
Out[136]: PLSRegression(copy=True, max_iter=500, n_components=9, scale=False, tol=1e-06)
In [137]: reg3.score(x[1::2, :], y[1::2])
Out[137]: 0.99979978303748307
In [138]: print((sqrt((reg3.predict(x[1::2, :]).squeeze() - y[1::2])**2).mean()))
0.124467834695
With such correlations (as shown by the figure and the condition number), multiple linear regression should be suboptimal. Yet when I use partial least squares, I get equal or worse results. Why doesn't my PLS1-regression perform better than ordinary linear regression?
The aim of the model is predictive; I am not trying to infer anything from regression coefficients.
In case anybody wants to have a closer look at the data, I have uploaded the explanatory matrix (1760 × 12) in to https://dl.dropboxusercontent.com/u/4650900/x.dat (516 kB) and the response variable to https://dl.dropboxusercontent.com/u/4650900/y.dat (43 kB), both in ASCII.