3

I have several datasets. Each dataset holds the masses of objects that have been subject to physical wear, expressed as a proportion of their original mass ($w$), and the amount of time that the object was exposed to physical wear ($t$). I assume that objects wear at a constant rate while they are exposed to wear, and that within a dataset, wear-rates are approximately Normally-distributed.

At some amount of wear, objects fail due to wear. Failed objects cannot be recovered, and so are not recorded in any dataset.

For each dataset, I wish to estimate:

  1. The mean wear-rate of objects within that dataset ($\mu$)
  2. The proportion of wear at which objects fail and become unobservable ($b$).

I have attempted a Bayesian approach to to estimating these parameters, as suggested in this question. When the dataset is affected by truncation, my current approach generates upward-biased estimates of $\mu$, and very imprecise estimates of $b$.

Code (R and JAGS):

points <- 1000

time <- runif(points, 0, 20000)  ## anything up to 20,000 days. For a 
                                  # dataset unaffected by
                                  # truncation, drop this to ~ 5000.
wearRates <- rnorm(points, (0.022/365), (0.0022/365))  
## typical wear-rates 
wear <- 1-(time*wearRates) 
losspoint <- 0.55  ## failure when 55% of initial mass remains
observable <- wear > losspoint

allPoints <- data.frame(time, wear, observable)
data <- subset(allPoints, observable == TRUE)

with(data, plot.default(wear ~ time
                  , ylim = c(0,1)
                  , ylab="Proportion mass remaining",
                  , col=rgb(0,0,0, alpha=0.2)
                  , pch = 16)
                  )
lines(lowess(data$time, data$wear, f = 0.1), type = "l", col=2, lwd = 2)
## plot of the generated data, with Lowess smoother. The smoother line
 # will show an 'elbow' if the dataset is strongly affected by truncation.

library(R2jags)
library(coda)

modelString="
model {
   #Likelihood
   for (i in 1:n) {
      w[i]~dlnorm(-mu*t[i], (sigma^2)*t[i]^2)T(b,1)
   }

# Priors
   mu ~ dnorm(0.022, 1.0E-8)
   b ~ dunif(0, 1)
   sigma ~ dunif(0,100)

# Derived parameters
   annualWear <- mu*365
}
"

writeLines(modelString, con="./wearModel.txt")

data.list <- with(data, list(w = wear, t = time, n = nrow(data)))
## dataset trimmed to a manageable size for JAGS
params <- c("mu", "b", "sigma", "annualWear")
nChains = 3
burnInSteps = 3000
thinSteps = 10
numSavedSteps = 15000
nIter = ceiling(burnInSteps+(numSavedSteps * thinSteps)/nChains)

data.r2jags <- jags(data = data.list,
                    inits = NULL,
                    parameters.to.save = params,
                    model.file = "./wearModel.txt",
                    n.chains = nChains,
                    n.iter = nIter,
                    n.burnin = burnInSteps,
                    n.thin = thinSteps)

print(data.r2jags)

plot(as.mcmc(data.r2jags))

Example:

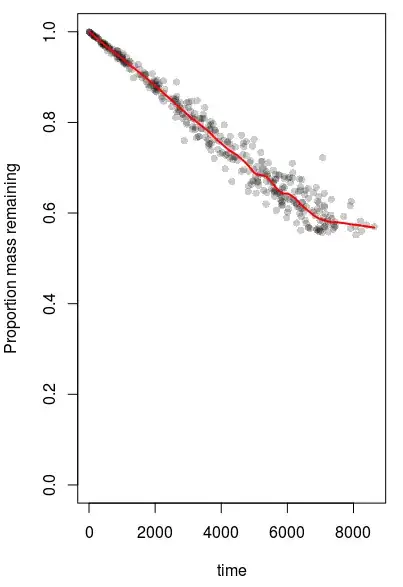
Here is a dataset affected by data-truncation due to wear (generated using the code above). Truncation is obvious from the characteristic 'elbow' in the Lowess smoother line. The value of b will therefore be near the lowest value of $w$ in this dataset (the value of $b$ is set to 0.55 in this example).

enter image description here

However, the posterior densities for b do not peak near the lowest value of $w$ as I expected them to. Also, the values of annualWear (which is defined as $\mu$*365) are estimated to be higher than they should be - annualWear is set to 0.022, not around 0.0265. annualWear appears to be more-accurately estimated in datasets that are unaffected by truncnation.

enter image description here

What am I doing wrong here?

Community
  • 1
bshane
  • 183
  • 7
  • I said in my answer to your original question that if you use w = 1 - r * t then you could follow my approach. By that I meant that you could follow the main steps, but you would have to modify some things. (Sorry if I was not clear about that.) In particular, the lognormal distribution for w is not correct in that case. Instead, the distribution is normal with a mean of 1 - mu * t and a standard deviation of sigma * t. This distribution can then be truncated at b and 1. – mef Mar 07 '16 at 12:37
  • You have to be careful about the arguments to dlnorm and dnorm. The second argument is the precision, not the variance. – mef Mar 07 '16 at 12:37
  • Unbiasedness is over-rated. Here's an example to illustrate that point. Flip a coin once. Suppose it comes up heads. Then the unbiased estimate of the probability of heads equals one! But it is not sensible to claim the probability of heads really is one based only on one coin flip. Any sensible answer must therefore be biased. If your prior for the probability were flat over the unit interval, then the mean of the posterior distribution would be 2/3. – mef Mar 07 '16 at 12:44
  • @mef: thanks for the clarifications. I've updated the formula, and the posterior for mu now looks like I expected it to (i.e., it slightly under-estimates mu when the data are truncated, owing to the imprecision of the estimate of b). My biggest concern with this model is accurately estimating b - at the moment, everything gives a flat posterior over the range of 0 -> b, rather than a spike at the correct point. – bshane Mar 08 '16 at 00:06
  • The posterior distribution for b that you are getting is not correct. I don't know why. I'm guessing the problem is in your JAGS code or with JAGS itself. There is a JAGS blog post that makes me wonder about truncation in JAGS: https://martynplummer.wordpress.com/2010/03/23/unknown-unknowns/. I have no problem getting a sensible distribution using my own Metropolis sampler. The distribution is asymmetric, with a smooth tail to the left and a sharp cutoff on the right at the minimum observed wear value. – mef Mar 08 '16 at 10:44

0 Answers0