0

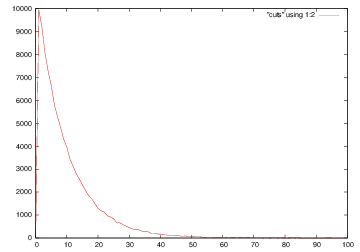
If I cut a string at random (uniformly distributed) positions, what is the distribution of lengths of the resulting fragments?

From what I understand the lengths should be distributed as a negative exponential (which my simulation below appears to confirm). I intuitively understand this as the probability of having encountered a break increases exponentially with length. Is this correct as this similar question suggests?

I have a collaborator who suggests this should be a Poisson distribution, is this incorrect? I assume the number of breaks in a region of the string is Poisson distributed is this correct?

Simulation I've simulated this with a string of length 1000000 and 100000 random cuts (I have also simulated with a fixed cut probability at each point and get similar results). I only cut at integral positions (my simulation creates a sequence, then adds cuts and calculates the length).

enter image description here

Community
  • 1
new299
  • 181
  • 2
  • It completely depends on what you mean by "random," which you haven't specified in your post. Your answer should follow immediately from whatever definition you choose. Also not sure what you mean by negative exponential. – dsaxton Mar 06 '16 at 02:11
  • @dsaxton I have updated the question to indicate the breaks are uniformly distributed. By negative exponential I mean this: https://en.wikipedia.org/wiki/Exponential_distribution – new299 Mar 06 '16 at 03:01
  • If the break is uniform then it's a tautology that the length is also uniform. Can you explain in a bit more detail how you did this simulation? – dsaxton Mar 06 '16 at 03:05
  • Indeed, for that matter how does the calculation whuber offered at the link you gave fail to be clear? What did you seek outside that derivation? – Glen_b Mar 06 '16 at 06:43

0 Answers0