Stock returns are a decent real-life example of what you're asking for. There's very close to zero correlation between today's and yesterday's S&P 500 return. However, there is clear dependence: squared returns are positively autocorrelated; periods of high volatility are clustered in time.
R code:
library(ggplot2)
library(grid)
library(quantmod)
symbols <- new.env()
date_from <- as.Date("1960-01-01")
date_to <- as.Date("2016-02-01")
getSymbols("^GSPC", env=symbols, src="yahoo", from=date_from, to=date_to) # S&P500
df <- data.frame(close=as.numeric(symbols$GSPC$GSPC.Close),
date=index(symbols$GSPC))
df$log_return <- c(NA, diff(log(df$close)))
df$log_return_lag <- c(NA, head(df$log_return, nrow(df) - 1))
cor(df$log_return, df$log_return_lag, use="pairwise.complete.obs") # 0.02
cor(df$log_return^2, df$log_return_lag^2, use="pairwise.complete.obs") # 0.14
acf(df$log_return, na.action=na.pass) # Basically zero autocorrelation
acf((df$log_return^2), na.action=na.pass) # Squared returns positively autocorrelated
p <- (ggplot(df, aes(x=date, y=log_return)) +
geom_point(alpha=0.5) +
theme_bw() + theme(panel.border=element_blank()))
p
ggsave("log_returns_s&p.png", p, width=10, height=8)
The timeseries of log returns on the S&P 500:
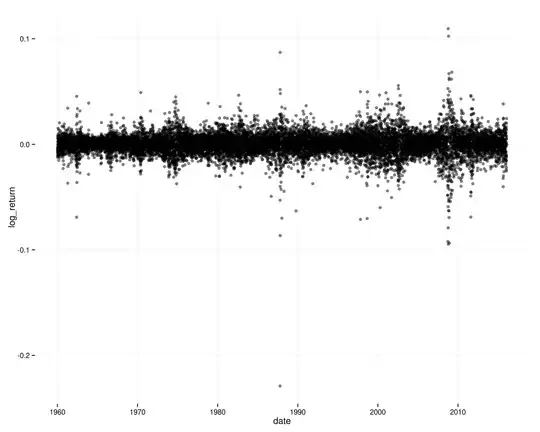
If returns were independent through time (and stationary), it would be very unlikely to see those patterns of clustered volatility, and you wouldn't see autocorrelation in squared log returns.
