I am currently making a short literature study of robust and efficient estimators. Some very well known are the median absolute deviation (MAD) and the interquartile range (IQR). However they both have a weakness for non-normal distributions, with the five number summary having at least the advantage of showing skewness through the box and whiskers plot.
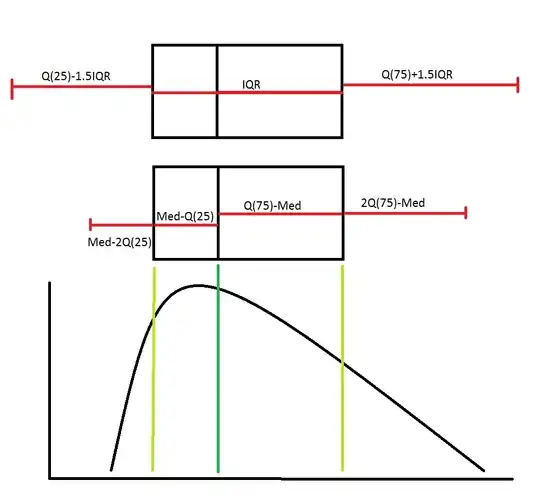
To me, it seems unreasonable to use the IQR, because it assumes same spacing both to the right and to the left of the corresponding quartile. In a distribution like the one shown below, this would cause a lot of "useless" information still to be included. (See Fig below, first box and whiskers plot)
What I would like to propose instead is to use the distance from the lower quartile to the median as an estimator for the standard deviation for values lower than the median, and the opposite for values higher than the median: $$ \text{if } x<\text{Med:} \ \text{reject if }|x−3(\text{Med}−Q(0.25))|>0 \\ \text{if } x>\text{Med:} \ \text{reject if } |x−3(Q(0.75)−\text{Med})|>0 $$ Of course, this method is quite robust (25%) and incredibly easy/fast to calculate. It would also follow the nature of the data when rejecting outliers.
What I would like to ask is if anybody else has seen this method applied somewhere else? It would also be great if somebody can help me find a way to calculate the efficiency of this method and/or mention its advantages/disadvantages.
Here a picture of what I am trying to say (only a spread of 2 s.d. are used in this case, to compare with the IQR it would be 3 s.d.):