thanks in advance for anyone taking the time to read/answer this.
I am comparing a ground-sourced dataset versus a satellite-sourced dataset for weather conditions, such as temperature. Both sets are time series data (ground takes a reading every 15 minutes while satellite is every 30 minutes, so there are twice as many data points from the ground data). I want to compare the difference between these two sets at each entry, to see if my ground data fits my satellite data to a statistical significance of whatever.
For example, a few entries for temperature would look like:
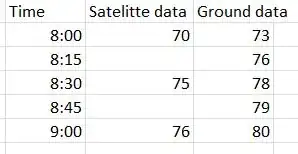
Basically, I am not sure which statistical test/method to use to determine if my ground data is 'good', or close enough to my satellite data, or how 'different' they are between each other to the point of inaccurate data.
The reason I ask is that the satellite data is much more reliable versus the ground data from some of the sites I am looking at, where sensor malfunctions plague my ground data sets. In essence, I want to automate this process in mathematica so that it will tell me if a dataset is worth using or not.
Thanks for all your help!