Imagine that you are given the mean and variance of a dataset but you do not know the distribution: Does it just the mean and variance give reasonable representation of the data? My guess is that it do not.
Ok, now they tell you that it is normal distributed. In this case you can infer everything with just the variance and mean, right?
But what about if it is not normal distributed? What about if you have this data:
Your example concerns with time-series data. Such data is bivariate by nature since you have information about actual values and time of their occurrence (see also this thread). If you compute mean and variance of the values, then you ignore the time of their occurrence. Moreover, in analyzing time-series data you are interested in finding time-patterns, so you assume that there is some dependence between the individual observations, that cannot be ignored.
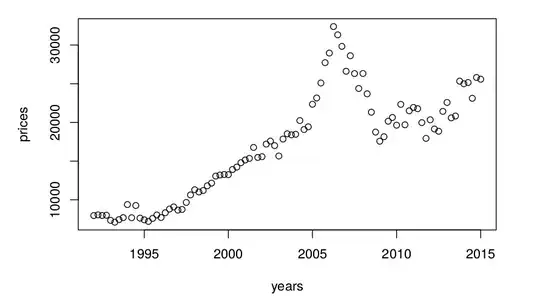
As an example let's look at the data about sheep population (in millions) of England and Wales from Forecasting: methods and applications by Makridakis, Wheelwright & Hyndman (1998). If you look at it, you can see a clear downward trend over time.
If you ignore the time and look at the distribution of sheep population counts, you will see that their distribution is approximately normal and describing it with mean and variance can be quite informative.
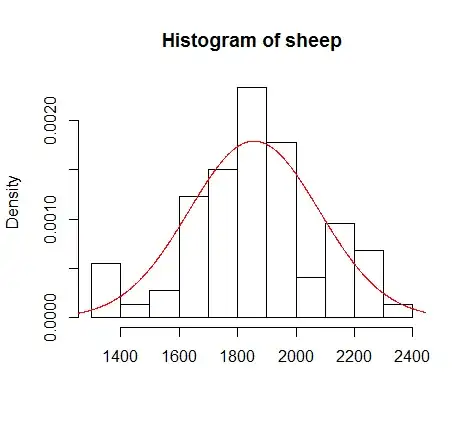
The plot above obviously does not tell you anything about how the sheep population changed over time. It tells you about the average sheep counts, their variability in given period etc.