What is the best way to decide bin size for computing Entropy or Mutual Information?

Question

I have a continuous distribution that I was thinking of binning for computing MI and H.

I often arbitrarily decide on bin size. Is there a general consensus on how to set bin size and number?

Thanks for your input!

Answer 1

One successful method to calculate number of bins (segments) in histogram method in order to estimate mutual information (MI) is :

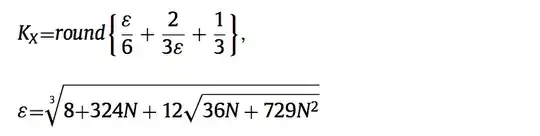I wrote code in python so here it is : (computing normalized MI (0,1))

def calc_MI(x, y, bins):
    # this hist function gives us the contigency of the elements of
    # the arrays in the chunks (bins) (segments).
    # so basically c_xy is a 2d array which every element is a
    # mutual contigency (if i can say) of x and y in that segment.
    c_xy = np.histogram2d(x,y,bins)[0]
    c_x = np.histogram(x,bins)[0]
    c_y = np.histogram(y,bins)[0]
    H_x = shan_entropy(c_x)
    H_y = shan_entropy(c_y)
    H_xy = shan_entropy(c_xy)
    MI = H_x + H_y - H_xy

    # normalized MI :
    MI = 2*MI/(H_x + H_y)

    return MI


def shan_entropy(c):
    # calculating the entropy (just like the formula)
    c_normalized = c / float(np.sum(c))
    c_normalized = c_normalized[np.nonzero(c_normalized)]
    H = -sum(c_normalized* np.log2(c_normalized))
    return H


# calculating number of bins with that paper........
def calc_bin_size(N):
    ee = np.cbrt(8 + 324*N + 12*np.sqrt(36*N + 729*N**2))
    bins = np.round(ee/6 + 2/(3*ee) + 1/3)

    return int(bins)

paper: A. Hacine-Gharbi, P. Ravier, "Low bias histogram-based estimation of mutual information for feature selection", Pattern Recognit. Lett (2012).