1

I have 2 series of data, for example:

s1: 0.3 0.3 0.4 0.8 0.6 0.5 0.7

s2: 0.7 0.7 0.6 0.8 0.7 0.5 0.6

It's easy to see that the data in s1 is fluctuating a lot (min=0.3, max=0.8) while in s2 all the values close to others.

Which metric should I use to measure the fluctuation like this? I tried with standard deviation but it's not very clear.

ula89
  • 13
  • 1
  • 1
  • 3
  • What's the problem with standard deviation? I get SD for s1 of 0.195 and for s2 of 0.098, which captures the contrast you rightly identify. – Nick Cox Feb 19 '16 at 11:05

3 Answers3

3

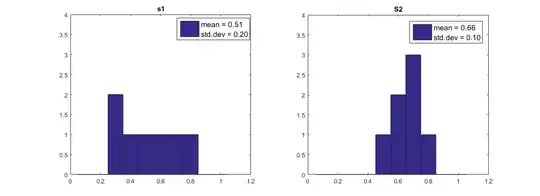
Depending on what exactly you are trying to measure, there could be a selection of metrics to choose. Standard deviation is indeed a good choice to measure the amount of variation or dispersion of a dataset.

The formula is typically given by:

$\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N} (x_i-\mu)^2 }$

where $N$ is the sample size, $x_i$ is each individual observation, and $\mu$ is the mean of the dataset.

Below I've plotted the two distributions, you can see that $\sigma_{s1}=0.2$ and $\sigma_{s2}=0.1$. This is telling you that on average, the data in s1 varies twice as much with respect to the mean value compared to s2. I encourage you to read up on the metric to gather a better understanding.

Edit:

As @NickCox has rightly pointed out, standard deviation is also commonly formulated as:

$\sigma = \sqrt{\frac{1}{N-1}\sum_{i=1}^{N} (x_i-\mu)^2 }$

Note that for relatively large sample sizes this will make little appreciable difference although please see this this answer for a discussion on the point.

enter image description here

Community
  • 1
CatsLoveJazz
  • 598
  • 1
  • 4
  • 22
  • Helpful. Note to those new to these ideas: Many people use $1/(N-1)$ rather than $N$, in the notation here. That convention underlies the results in my comment on the question. Also _number of samples_ is common wording in some sciences, but _sample size_ or _number of observations_ is more likely wording from statistical texts or courses. – Nick Cox Feb 19 '16 at 11:57
  • Yes indeed you are absolutely correct @NickCox, I believe the merits of both formulations can be discussed late into the night by statisticians...guess you can spot the engineer with sloppy jargon and *close enough* approach. I'll update my answer to note these points more clearly for future readers. – CatsLoveJazz Feb 19 '16 at 12:59
1

Standard deviations are not scale invariant, i.e., they are expressed in the units of the measure. For a scale invariant metric that is dimensionless and comparable across measures that differ widely in location and scale, use the coefficient of variation. The CV is calculated as the std dev divided by the mean times 100.

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Mike Hunter
  • 9,682
  • 2
  • 20
  • 43
  • 1
    Clearly correct in what you say. But here the units of measurement are evidently the same. When that is so the SD having the same units of measurement as the data is not a problem, and indeed is arguably a real feature. The coefficient of variation is most useful whenever variation is essentially multiplicative, i.e. SD/mean really is approximately constant. That doesn't appear so here. – Nick Cox Feb 19 '16 at 13:19
  • @NickCox Thanks for the clarifying edits. Fair point but consider this: prices of two stocks are both valued in dollars (the same unit of measure) but differ widely in their mean and std deviations. So, stock 1 has an average of 500 dollars with a std deviation of 50 while stock 2 has an average of 5 dollars with a std deviation of 10. Which stock has more variability? – Mike Hunter Feb 19 '16 at 13:49
  • 1
    The example undermines nothing I said. Indeed the CV is widely used in biology to compare mice and elephants, figuratively speaking. The answer to your question is naturally that there are different measures of variability and people should focus on what helps them most in their problem, but it's really not a good idea if anyone assumes that variability is a single scalar phenomenon to be measured in just one correct way. (If the mean price is 5 and the SD is 10, the stock is probably doomed any way.) – Nick Cox Feb 19 '16 at 15:46
  • @NickCox Ha, ha...right you are about stock 2 -- bad example but the main point stands. Suggesting that I suggested that there is "one correct way" to measure variability would, of course, be a misinterpretation of my comment. – Mike Hunter Feb 19 '16 at 16:01
  • Quite so. That is why I said "if anyone assumes". That cap evidently doesn't fit you, but the broad point remains that "more variability" can't be assigned without deciding on the measure. We don't disagree about any principle, I trust; I sense that you would use the CV much more frequently than I would, but that's a matter of taste and style to some extent. – Nick Cox Feb 19 '16 at 16:06
  • @nickcox Yes, I use it whenever it's appropriate and particularly in evaluating the variability in time series such as equities. It's really quite, quite a powerful, underutilized metric. – Mike Hunter Feb 19 '16 at 16:08
  • Mileages do vary. I've seen some extraordinary misuses, none with your name on them. For an attempt at even-handedness, see http://stats.stackexchange.com/questions/118497/how-to-interpret-the-coefficient-of-variation – Nick Cox Feb 19 '16 at 16:53
1

I would suggest that you need to understand the underlying distribution of the data first before determining what measure of variability to use. So it's not a simple as saying it's "standard deviation".

Certainly for Normal distributions, standard deviation is a good one. I personally use +/- 2 standard deviation for comparison if I do want to find a difference, or +/- 3 standard deviation for comparison if I don't want to find a difference.

Standard deviation as defined for Normal Distribution wouldn't work for Binomial Distribution (coin flipping e.g.). The standard deviation is based on the probability of either event happening.

Std Deviation as defined for Normal Distribution also doesn't work for Poisson Distribution (length of a queue e.g.), though using the central limit theorem, your distribution can approximate a Normal.

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Marcus D
  • 259
  • 1
  • 4
  • 11