Symmetry of Partial correlation

Question

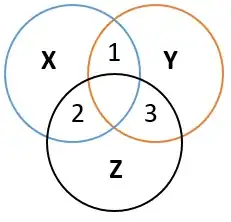
Inspired by the question and the diagram represented in the answer, I am wondering if partial correlation is symmetric?

We know that $\rho(X,Y) = \rho(Y,X)$. See here.

From ,

we know that $\rho_{XY|Z} = \sqrt{ \frac{Area(1)} {Area(Y-(3+Center))} }$. Similarly, we can say $\rho_{YX|Z} = \sqrt{ \frac{Area(1)} {Area(X-(2+Center))} }$.

The questions then are as follows:

1. Are the sizes of $X$, $Y$, and $Z$ in the diagram related to the measures of the sets ${X,Y,Z}$ respectively?
2. I would think that because the denominators are not guaranteed to be the same, that $\rho_{XY|Z}$ is not always equal to $\rho_{YX|Z}$?

Answer 1

Look at https://en.wikipedia.org/wiki/Partial_correlation . The partial correlation between $X$ and $Y$ controlling for $Z$ (which might be a vector, written $\rho_{XY\cdot Z}$, can be defined in the following way.

Compute first the linear regression of $X$ on $Z$, then the linear regression of $Y$ on $Z$. Then calculate the two vectors of residuals in the two models, written respectively $e_X, e_Y$. Then the partial correlation is given by $$ \rho_{XY\cdot Z} = \text{corr}(e_X,e_Y) $$ The usual correlation used in the formula above is clearly symmetric in its two arguments, and that will carry over to the partial correlation. So the answer to the question is, YES, partial correlation is also symmetric.