Probability two people arrive at the same time?

Question

Two people arrive at a train station at a random time between 12pm and 1pm. They arrive independently of each other and their arrival times are uniformly distributed. What is the probability they arrive at exactly the same time? I am trying to use a graphical approach, and just have straight line (y=x). Wouldn't this yield a probability of zero, since the area of a line is 0?

Answer 1

Let's start with simple case with discrete time. If you have two discrete random variables $X$ and $Y$ that that are iid and follow discrete uniform distributions with $k$ possible categories (arrival times from $0$ to $k-1$), then probability of $X=x$ is $1/k$ and the same for $Y$. Since $X$ and $Y$ are independent, then $\Pr(X=t \cap Y=t) = \Pr(X=t)\times\Pr(Y=t) = 1/k^2$.

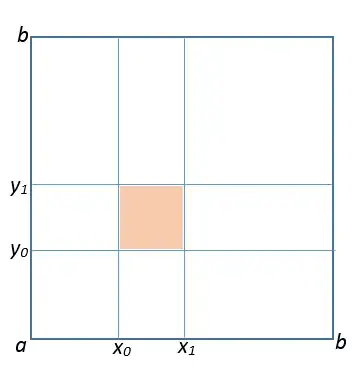
With continuous variables things get more complicated (and I assume that if you are talking about time you think of continuous time). For continuous random variable $X$ probability of $X=x$ for any $x$ is equal to zero (that is why we use pdf's instead of pmf's). So for continuous line from $a$ to $b$ point $x$ occupies infinitesimal space. If you align two such lines $X$, $Y$ than the probability of $X=t$ and $Y=t$ occurring simultaneously goes to zero as probability of each of the events alone is zero. With a single variable we were talking about a line and with two variables we can think of it as of square, with $\Pr(X=x \cap Y=y)$ being a single point inside such square.

What you could do is to compute probability of two arrivals occurring within some time interval (say $\pm \varepsilon$), by using cumulative distribution functions

$$ \Pr(t-\varepsilon \le X \le t+\varepsilon \cap t-\varepsilon \le Y \le t+\varepsilon) \\ = \left( F_X(t+\varepsilon) - F_X(t-\varepsilon) \right) \times \left( F_Y(t+\varepsilon) - F_Y(t-\varepsilon) \right)$$

What translates to talking about area of smaller square within bigger square.