I am implementing PCA, LDA, and Naive Bayes, for compression and classification respectively (implementing both an LDA for compression and classification).
I have the code written and everything works. What I need to know, for the report, is what the general definition of reconstruction error is.
I can find a lot of math, and uses of it in the literature... but what I really need is a bird's eye view / plain word definition, so I can adapt it to the report.
For PCA what you do is that you project your data on a subset of your input space. Basically, everything holds on this image above: you project data on the subspace with maximum variance. When you reconstruct your data from the projection, you'll get the red points, and the reconstruction error is the sum of the distances from blue to red points: it indeed corresponds to the error you've made by projecting your data on the green line. It can be generalized in any dimension of course!
As pointed out in the comments, it does not seem that simple for LDA and I can't find a proper definition on the internet. Sorry.
The general definition of the reconstruction error would be the distance between the original data point and its projection onto a lower-dimensional subspace (its 'estimate').
Source: Mathematics of Machine Learning Specialization by Imperial College London
What I usually use as the measure of reconstruction error (in the context of PCA, but also other methods) is the coefficient of determination $R^2$ and the Root Mean Squared Error (or normalised RMSE). These two are easy to compute and give you a quick idea of what the reconstruction did.
Let's assume $X$ is your original data and $f$ is the compressed data.
The $R^2$ of the $i^{th}$ variable can be computed as:
$R^2_i = 1 - \frac{\sum_{j=1}^n (X_{j,i} - f_{j,i})^2}{\sum_{j=1}^n X_{j,i}^2}$
Since $R^2 = 1.0$ for a perfect fit, you can judge the reconstruction by how close the $R^2$ is to 1.0.
The RMSE of the $i^{th}$ variable can be computed as:
$ \text{RMSE}_i = \sqrt{\overline{(X_i - f_i)^2}} $
which you can also normalise by a quantity that suits you (norm $N$), I often normalise by the mean value, the NRMSE is thus:
$\text{NRMSE}_i = \frac{\text{RMSE}_i}{N_i} = \sqrt{\frac{\overline{(X_i - f_i)^2}}{\overline{X_i^2}}}$
In case you are using Python you can compute these as:
from sklearn.metrics import r2_score
from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np
r2 = r2_score(X, f)
rmse = sqrt(mean_squared_error(X, f))
# RMSE normalised by mean:
nrmse = rmse/sqrt(np.mean(X**2))
where X is the original data and f is the compressed data.
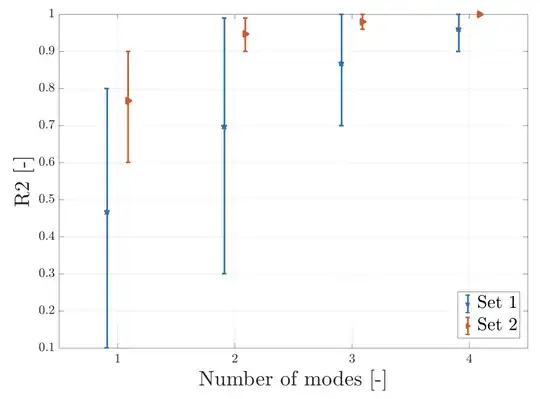
In case it is helpful for you to do some sensitivity analysis you can then judge visually how the $R^2$ or RMSE change when you change parameters of your compression. For instance, this can be handy in the context of PCA when you want to compare reconstructions with increasing number of the retained Principal Components. Below you see that increasing the number of modes is getting your fit closer to the model:
Bird eye view for Reconstruction error in the PCA context will be variability of the data which we are not able to capture.
Notation Principle subspace - lower dimensional subspace on which data is projected
In PCA Reconstruction error or loss is sum of eigen values of the ignored subspace. Lets say you have 10 Dimensional data, and you are selecting first 4 principal components, what this means is your principle subspace has 4 dimensions and corresponds to 4 largest eigen values and respective vectors, So reconstruction error is sum of 6 eigen values of the ignored subspace, (the smallest 6).
Minimizing the reconstruction error means minimizing the contribution of ignored eigenvalues which depends on the distribution of the data and how many components we are selecting.
Ignored subspace is orthogonal complement of principal subspace, so reconstruction error can be seen as average squared distance between the original data points and respective projections onto principal subspace as shared in another answer.
