Features, samples, and over-fitting?

Question

I have a data set with 30 samples, 2 classes, and 100,000 features. When I run an SVC classifier on it from SKLearn using stratified cross-validation, the accuracy is barely better than chance.

After running recursive feature elimination with cross validation (RFECV in SKLearn), it reduces the number of features to 5000, which is still a lot. My accuracy increases to 95%.

I assume my model is likely over-fit, given the features/sample ratio. However, wouldn't the model be more over-fit with 100,000 features (even if the majority of these features are noise) than with 5000 features? In which case, why does the accuracy jump greatly with the decrease in features? Is the relationship between #-of-features, over-fitting, and resulting accuracy a non-linear relationship?

Answer 1

Let's start from a different scenario: a set of points that is not linearly separable.

A projection (mapping) onto a higher dimensional space can allow us linearly separate our data.

Let's stretch this idea. Let's project data onto a extremely high dimensional data. The planar separator in the extremely-high-dimensional space of feature vectors will be a curved (highly non-linear) separator in the low dimensional space. We are therefore very likely introducing over-fitting.

What we have described is a clear trade-off between bias and variance.

I forgot to mention that there's a bound in the parametrization of the separating hyperplanes:

if we are in a space $\mathcal{H}$, the set of hyperplanes is parametrized by $dim( \mathcal{H} ) + 1$. However, given the form of solution [of the SVM], there are at most $l$ + 1 adjustable parameters (where $l$ is the number of training samples) (source)

Note that there's a relationship between the number of support vectors and model complexity:

Now, the number of support vectors still depends on how much slack we allow, but it also depends on the complexity of our model. Each twist and turn in the final model in our input space requires one or more support vectors to define. ... The number of support vectors can range from very few to every single data point if you completely over-fit your data. This tradeoff is controlled via C and through the choice of kernel and kernel parameters. (source)

This is the higher level big picture on the trade-off and the risk of poor generalization in a high dimensional problem. See the answer below by Dikran Marsupial for a more detailed description of the role of feature selection in this context.

Answer 2

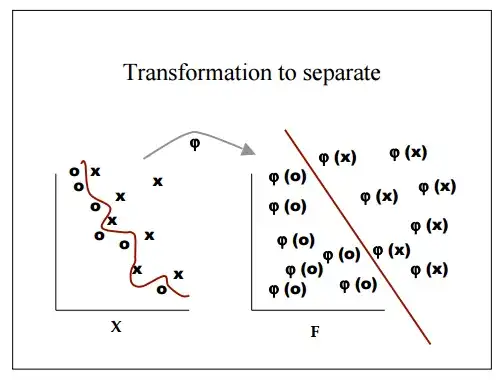
The SVM (strictly speaking the maximum margin hyperplane) is an approximate implementation of a bound on generalisation performance that is independent of the dimensionality of the feature space. This means that in principle, the SVM is able to perform well in high dimensional space (i.e. lots of features for a linear SVM). However, in practice, this is highly dependent on choosing a good value for the regularisation parameter (usually $C$) which controls the trade-off between minimising the error (as measured by the hinge loss) on the training data, and maximising the margin (which maximises bound on generalisation perfomance). So, the best approach is probably to use a linear classifier, and carefully tune $C$ to minimise the cross-validation error (or the span bound, or radius margin bound), and then have an independent test set for estimating generalisation performance (or as the dataset is small, use nested cross-validation).

The problem with using feature selection is that while the SVM is based on a generalisation bound that helps avoid over-fitting, no such bound applies to the feature selection step (and indeed the feature selection step invalidates the bound on which the SVM is based). This means feature selection is likely to make generalisation performance worse as you just over-fit the feature selection procedure.

If all that is important is generalisation performance, then don't do any feature selection, and carefully tune $C$ so the model is properly regularised. For most datasets, that seems to be a good approach, but there are some where feature selection is also beneficial in addition to careful regularisation.