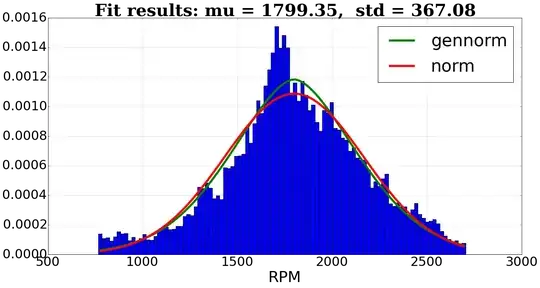
I've a dataset with about 12k values given. It looks like this:
When I try to test for normality I get following results, where p-value is extremely slow:
NormaltestResult(statistic=93.328975616353148, pvalue=5.4183922830109284e-21)
ShapirotestResult(0.9910582304000854, 9.806942512599108e-26)
(values for distribution curve fitting)
Searching best parameters for distribution gennorm (error 1.63000230512e-06)
Searching best parameters for distribution norm (error 2.16497464839e-06)
sumsquare_error
gennorm 0.000002
norm 0.000002
Am I wrong about thinking it is normally distributed because I get such low p-values?