It is a straightforward approach having a set of coordinates (e.g., in 2D as {x,y}) and at least an associated variable (e.g., v) to calculate a variogram as a descriptor of the spatial dependency of the variable v through the field being studied.
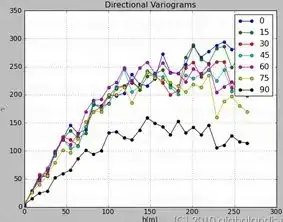
The question appeared to me is:
how to generate a realization of a dataset having a variogram? (inverse move!)
That is, there is at least one variogram available but neither dataset nor other description is available and the goal is to generate a realization of original (unknown) dataset that could have such a variogram.
What is the probability of having such a realization?
Updates / Comments:
From variogram in the above context I mean empirical variogram. I suppose that fitting a variogram model is not an issue at least for this question.
Also variogram is available as pairs (h, gamma).