11

Suppose I have a simple single layer neural network, with n inputs and a single output (binary classification task). If I set the activation function in the output node as a sigmoid function- then the result is a Logistic Regression classifier.

In this same scenario, if I change the output activation to ReLU (rectified linear unit), then is the resulting structure same as or similar to an SVM?

If not why?

Franck Dernoncourt
  • 42,093
  • 30
  • 155
  • 271
A.D
  • 2,114
  • 3
  • 17
  • 27
  • do you have any hypothesis on why that might be the case? the reason why a single perceptron = logistic is exactly because of the activation - they are essentially the same model, mathematically (although maybe trained differently) - linear weights + a sigmoid applied to the matrix multiplication. SVMs work quite differently - they seek the best line to separate the data - they are more geometric than "weighty"/"matrixy". For me, there is nothing about ReLUs that should make me think = ah, they are same to an SVM. (logistic and linear svm tend to perform very similarly though) – metjush Jan 15 '16 at 20:11
  • the max-margin objective of an svm and the relu activation function look the same. Hence the question. – A.D Jan 15 '16 at 21:49
  • " SVMs work quite differently - they seek the best line to separate the data - they are more geometric than "weighty"/"matrixy". thats a little hand-wavy - ALL linear classifiers seek the best line to separate the data including logistic regression and perceptron. – A.D Jan 15 '16 at 21:50
  • Generally speaking, learning = representation + optimization + evaluation so that when it comes that two learning algorithms are equal, it means that these three components are equal. The SVM with kernel trick is related with the neural network as shown in the [Support vector network](https://link.springer.com/article/10.1007/BF00994018). – 张子一 Jun 26 '20 at 16:08

1 Answers1

11

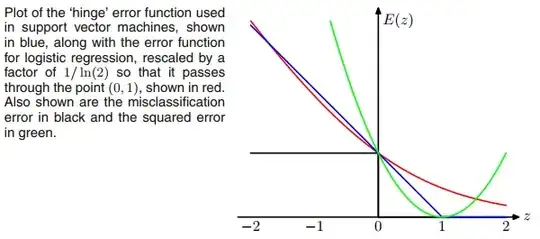
Maybe what makes you think of ReLU is the hinge loss $E = max(1-ty,0)$ of SVMs, but the loss does not restrict the output activation function to be non-negative (ReLU).

For the network loss to be in the same form as SVMs, we can just remove any non-linear activation functions off the output layer, and use the hinge loss for backpropagation.

Moreover, if we replace the hinge loss with $E = ln (1 + exp(−ty))$ (which looks like a smooth version of hinge loss), then we'll be doing logistic regression as typical sigmoid + cross-entropy networks. It can be thought of as moving the sigmoid function from the output layer to the loss.

So in terms of loss functions, SVMs and logistic regression are pretty close, though SVMs use a very different algorithm for training and inference based on support vectors.

There's a nice discussion on the relation of SVM and logistic regression in section 7.1.2 of the book Pattern Recognition and Machine Learning.

enter image description here

dontloo
  • 13,692
  • 7
  • 51
  • 80
  • thanks for pointing to the book. So I am getting a sense that apart from activation functions, the real difference is in the optimization algorithms used. For LR we can use simple unconstrained gradient descent, while in SVM we typically solve a constrained optimization. – A.D Jan 18 '16 at 19:36