1

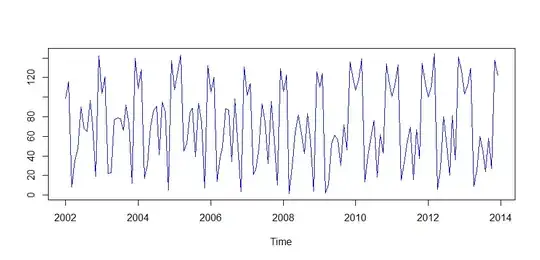
I have this monthly time series with pronounced seasonality and a bit of trend:

enter image description here

The ACF and PACF for 4 years (48 months) are:

enter image description here

  1. Can I suppose that the data don't need transformations like: log(data), diff(data)...?

    ACF: A spike at lag 12 in the ACF but no other significant spikes.
    PACF: ?

  2. R proposes ARIMA(0,0,0)(1,0,0)[12]. Could it be a good model?

Community
  • 1
user4563174
  • 25
  • 7
  • 1. Depends on the model you plan to use. Traditional ARMA assumes stationary normality – Zachary Blumenfeld Jan 07 '16 at 01:39
  • If your using an ARMA and the data is not stationary and/or not well approximated with a conditional normal then you would want to transform it. In your case it is hard to tell (about the normality part...it looks stationary. You could formally test stationarity if it would make you feel better though). The resulting ARMA would assume it is possible for the series to go below 0. If that is not posible with your data and the ARMA forecasts/fitted values go below 0 then maybe log transform. 2. Cannot be answered until you define what "good" means – Zachary Blumenfeld Jan 07 '16 at 01:49

2 Answers2

1

It looks like a plausible model, though I'd possibly start with seasonal differencing and see if the residuals from that didn't look over-differenced.

If you do go with the suggested model you have, you'd still look to see if there was autocorrelation in the residuals.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Regarding the first sentence of the answer: I guess the function `auto.arima` was used to arrive to `ARIMA(0,0,0)(1,0,0)[12]`. If I am not mistaken, it tests for a seasonal unit root on the way, so if it did not suggest one, the test must have indicated absense of seasonal unit root. – Richard Hardy Jan 07 '16 at 08:36
  • @Richard (edit) You are right, it uses the [Osborn-Chui-Smith-Birchenhall test](http://stats.stackexchange.com/questions/30220/how-does-rs-auto-arima-function-determine-the-order-of-differencing-when-esti). [The discussion of deterministic seasonality in that paper would mean -- if I understand the paper right -- that deterministic seasonality could still be present.] – Glen_b Jan 07 '16 at 10:52
0

Based on the text here, you will need to compute the p-value and thus identify if there your time series is stationary.

sandyp
  • 426
  • 1
  • 3
  • 11