Suppose we have two real-valued random variables $X,Y$. Let $cdf_X$ and $cdf_Y$ be the corresponding cumulative distribution functions. We are interested in graphically comparing the distributions of $X$ and $Y$.
If we plot the set of points $$(cdf_X^{-1}(z),cdf_Y^{-1}(z))$$ for some $z\in[0,1]$, the resulting graph is called a Q-Q plot. If $cdf_X=cdf_Y$, then the Q-Q plot lies along the $\textbf{x=y line}$ on the graph.
The Q-Q plot is very useful, but if $X$ or $Y$ have a few extremal values that differ, the plot can be somewhat visually misleading. For example, suppose $X$ is a uniform distribution over 1000 samples drawn from a standard normal distribution. $Y$ is generated the same way, with independent samples. Here is a corresponding QQ-plot; note that the points in the upper right and lower left corners wander off the dotted $\textbf{x=y line}$.
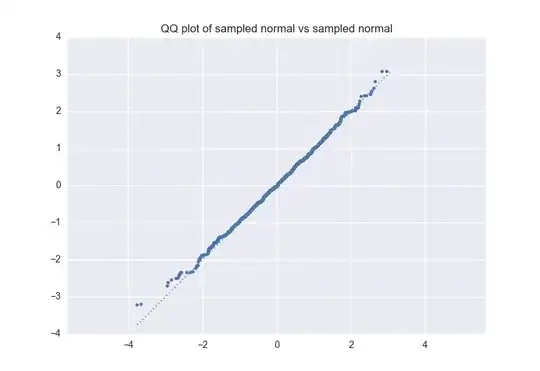 Although the extremal points diverge, there aren't many of them. In order to display the alignment of the majority of the points, we could instead plot
$$(z,cdf_Y(cdf_X^{-1}(z)))$$
Here is the corresponding "inverse Q-Q plot"; because the majority of points align well, it is more visually obvious (to me, anyway) that the distributions are similar.
Although the extremal points diverge, there aren't many of them. In order to display the alignment of the majority of the points, we could instead plot
$$(z,cdf_Y(cdf_X^{-1}(z)))$$
Here is the corresponding "inverse Q-Q plot"; because the majority of points align well, it is more visually obvious (to me, anyway) that the distributions are similar.

I haven't run across the "inverse Q-Q plot" before, but it's sufficiently natural that it's probably a standard tool. Does this plot have a name?