Why is the noncentral chi-squared approximate of the deviance bad?

Question

The statistical model under consideration is given by the independent realizations of two independent binomial distributions: $$ x_1 \sim \mathrm{Bin}(n_1, p_1), \quad x_2 \sim \mathrm{Bin}(n_2,p_2), $$ and the null hypothesis is $H_0\colon\{p_1=p_2\}$.

According to my calculations, the deviance (minus double log-likelihood ratio) has a noncentral chi-squared asymptotic distribution with $1$ degree of freedom and noncentrality parameter $$\lambda = \frac{{(p_1-p_2)}^2n_1n_2}{n_1p_2(1-p_2) + n_2p_1(1-p_1)}.$$

dev <- function(n1,x1,n2,x2){
  2*(x1*log(x1/n1) + (n1-x1)*log(1-x1/n1) + x2*log(x2/n2) + (n2-x2)*log(1-x2/n2) - (x1+x2)*log((x1+x2)/(n1+n2)) - (n1+n2-(x1+x2))*log(1-(x1+x2)/(n1+n2)))
}
lambda <- function(n1,p1,n2,p2){
  (p1-p2)^2 * (n1*n2)/(n1*p2*(1-p2)+n2*p1*(1-p1))
}

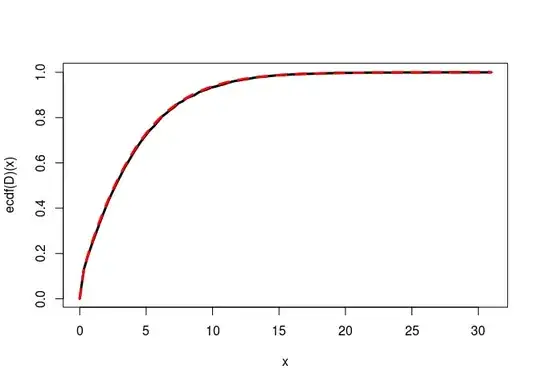
Simulations on the following example perfectly fit the noncentral chi-squared:

n1 <- 150; n2 <- 100
p1 <- 0.3; p2 <- 0.4 
nsims <- 15000
D <- numeric(nsims)
for(i in 1:nsims){
  x1 <- rbinom(1, n1, p1); x2 <- rbinom(1, n2, p2)
  D[i] <- dev(n1, x1, n2, x2)
}
curve(ecdf(D)(x), from=min(D), to=max(D),lwd=3)
ncp <- lambda(n1, p1, n2, p2) 
curve(pchisq(x, df=1, ncp=ncp), add=TRUE, col="red", lty="dashed", lwd=3)

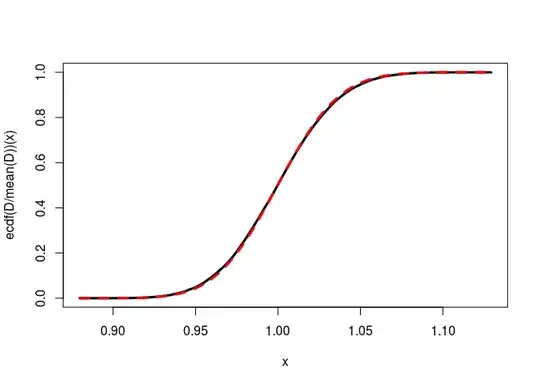
But when I increase the difference $|p_1-p_2|$, this is bad:

p1 <- 0.3; p2 <- 0.7 
for(i in 1:nsims){
  x1 <- rbinom(1, n1, p1); x2 <- rbinom(1, n2, p2)
  D[i] <- dev(n1, x1, n2, x2)
}
curve(ecdf(D)(x), from=min(D), to=max(D),lwd=3)
ncp <- lambda(n1, p1, n2, p2) 
curve(pchisq(x, df=1, ncp=ncp), add=TRUE, col="red", lty="dashed", lwd=3)

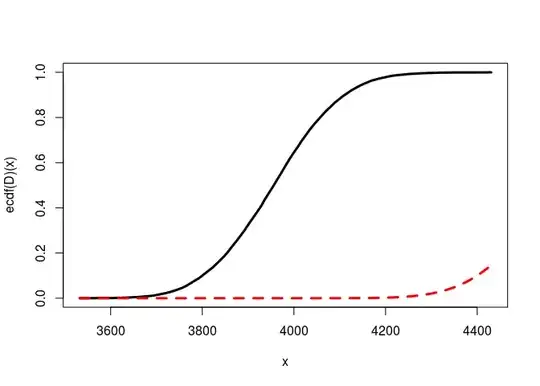
And this is worst when I increase the sample sizes:

n1 <- 15000; n2 <- 10000
for(i in 1:nsims){
  x1 <- rbinom(1, n1, p1); x2 <- rbinom(1, n2, p2)
  D[i] <- dev(n1, x1, n2, x2)
}
curve(ecdf(D)(x), from=min(D), to=max(D), lwd=3)
ncp <- lambda(n1, p1, n2, p2) 
curve(pchisq(x, df=1, ncp=ncp), add=TRUE, col="red", lty="dashed", lwd=3)

I have checked there's no problem with pchisq even for a large ncp. So why is it so bad ?

I also think there is no problem in the calculation of the deviance, because results are the same when replacing it by its Pearson approximate which does not involve logarithms.

Hmm.. that suggests there's something which holds only under $H_0$ in my approximate... I don't think so but I have to check. — Stéphane Laurent, Jan 02 '16 at 13:14

score 2 · Answer 1 · answered Jan 02 '16 at 20:17

In fact, I think this approximation is not as bad as it looks.

Take the third case, the worst one. The "absolute divergence" which is apparent on the figure looks big, but if I compare the distribution of the deviance normalised by its mean with the noncentral chi-squared normalised by its mean ($ncp+1$), then they look to be close :

curve(ecdf(D/mean(D))(x), from=min(D/mean(D)), to=max(D/mean(D)), lwd=3)
ncp <- lambda(n1, p1, n2, p2) 
curve(pchisq(x*(ncp+1), df=1, ncp=ncp), add=TRUE, col="red", lty="dashed", lwd=3)

Why is the noncentral chi-squared approximate of the deviance bad?

1 Answers1