I have a third party random number generator with a period approximately greater than $63*(2^{63} - 1)$ which generates numbers in the range $[0,2^{32}-1]$, ie $2^{32}$ different numbers. I've made some slight modifications and wish to verify its distribution remains uniform. I am using Pearson's chi-squared test for fit of a distribution, hopefully correctly, without knowing much about it:
Divide $1000*2^{32}$ observations across $2^{32}$ different discrete cells (I figure the number of observations $n$ should be $5*2^{32} \lt n \lt 63*(2^{63} - 1)$, or, $5*\text{range} \lt n \lt \text{periodicity}$, using the five-or-more-rule, to gain decent confidence). The expected theoretical frequency $E_i = 1000*2^{32} / 2^{32} = 1000$.
the reduction in degrees of freedom is 1.
$x^2 = \sum_{i=0}^{2^{32}-1}(O_i - E_i)^2/E_i$.
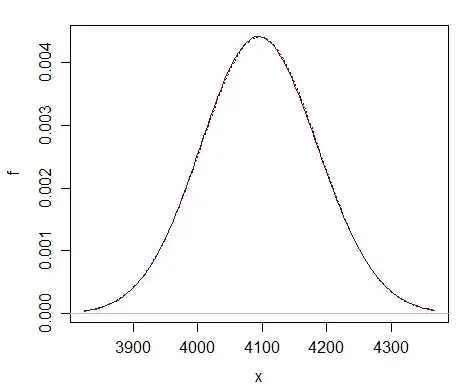
degrees of freedom = $2^{32} - 1$.
lookup the p-value of a chi-squared ($x^2$) distribution given $2^{32} - 1$ degrees of freedom.
As far as I can tell, no chi-squared distribution exists for that many degrees of freedom. What should I do?
select a
confidencesignificance value $c$ such that $p > c$ signifies the distribution is probably uniform. I have a large sample size but since I'm unsure of its relation to p-value (increased sampling reduces errors but significance value represents a ratio in the types of errors) I think I'll just stick with the standard value 0.05.
Edit: actual questions italicized above, and enumerated below:
- How to get a p-value?
- How to select a significance value?
Edit:
I've asked a follow-up question at chi-squared goodness-of-fit: effect size and power.