An example like the t-distribution with 2 degrees of freedom would not suffice as the second moment exists but equals inf.
-
6This will not be possible: the even moments of a non-negative measurable function are either (non-negative) finite or (positive) infinite. – Henry Nov 20 '11 at 15:06
-
@Henry (+1): You beat me to it. :) – cardinal Nov 20 '11 at 15:07
-
@Henry: Please consider expanding a bit on your comment in an answer. I think it makes an important point and I, for one, will be upvoting. (Of course, I'm the last person to be twisting anyone's arm to submit comments as answers.) :) – cardinal Nov 23 '11 at 22:15
-
1@cardinal - I won't object if you make the point in an answer yourself – Henry Nov 23 '11 at 22:25
2 Answers
I think there is a confusion due to the fact that the distribution $t(1)$ ($t$ with 1 degree of freedom) has no mean, even if you accept values in $\overline{\mathbb R} = \mathbb R \cup \{ -\infty, +\infty \}$.
An indefinite integral like $$ E(X) = \int_{-\infty}^{+\infty} x f(x) \mathrm dx $$ is defined as the sum of the two following limits: $$ \int_0^{+\infty} x f(x) \mathrm dx = \lim_{T\rightarrow+\infty} \int_0^T x f(x) \mathrm dx, $$ $$ \int_{-\infty}^0 x f(x) \mathrm dx = \lim_{T\rightarrow-\infty} \int_T^0 x f(x) \mathrm dx.$$ If both limits are finite, it is well defined.
As $f(x)$ is a density, it is non-negative, and a $x f(x)$ has constant sign on $(-\infty,0]$ and $[0,\infty)$, hence if you accept values in $\overline{\mathbb R}$, it is possible to have infinite limits $ \int_0^{+\infty} x f(x) \mathrm dx = +\infty$ and $\int_{-\infty}^0 x f(x) \mathrm dx = -\infty$. If both are infinite then their sum is indefinite, even if you accept infinite values.
Concretely, on the following picture (graph of $xf(x)$ with $f$ the density of the $t$-distribution with one df) the positive ane negative areas are infinite, so their sum is indefinite.
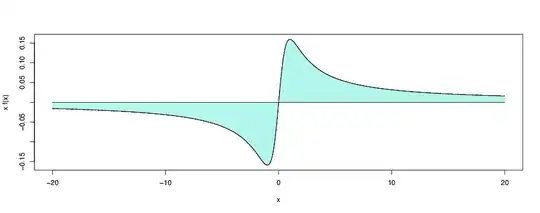
However when dealing with the second moment $$ E\left( X^2 \right) = \int_{-\infty}^{+\infty} x^2 f(x) \mathrm dx,$$ as we have $x^2 f(x) \ge 0$ for all $x$, if the limits $$ \int_0^{+\infty} x^2 f(x) \mathrm dx = \lim_{T\rightarrow+\infty} \int_0^T x^2 f(x) \mathrm dx, $$ $$ \int_{-\infty}^0 x^2 f(x) \mathrm dx = \lim_{T\rightarrow-\infty} \int_T^0 x^2 f(x) \mathrm dx,$$ are not finite, they necessarily go to $+\infty$, hence either $E\left(X^2\right)$ is finite, or it is $+\infty$ if you accept values in $\overline{\mathbb R}$.
Concretely, the area under a curve which is always in the upper half plane is always defined in $\mathbb R \cup \{+\infty\}$. On the following picture (graph of $x^2 f(x)$ with $f$ the density of the $t$ distribution with 2 df), it is infinite.
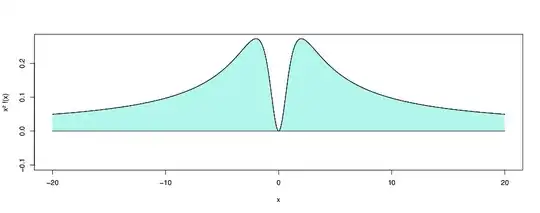
- 11,870
- 36
- 56
-
1+1 Great illustrations. They make one think: on a computer there will be limits to the size of numbers that can be represented and usually they will be symmetric. In that case we actually have a truncated distribution. By the same argument, it *does* have a mean and the mean is zero! I am moved to ask: to what extent should one be concerned about a behavior that truly happens at infinity when working on practical problems that necessarily use finite numbers? I'm not fishing for an answer--I can think of plenty of rejoinders--but just want to put that idea out there for general consideration. – whuber Jan 19 '12 at 22:41
-
1@whuber Thanks for thoughtful comments. It is indeed true that in practice, a centered distribution with huge variance for which we have only small finite samples, or a distribution without a first moment... I don’t think it makes no difference. Actual and potential infinites... I am sure you remember this question :[test for finite variance](http://stats.stackexchange.com/questions/2504/test-for-finite-variance) where you and Henry gave nice answers. – Elvis Jan 19 '12 at 22:51
-
It is unsettling to see a graph with axis labeled $f(x)$ and the curve dipping below the horizontal axis. Could you please change the label to $xf(x)$ and say more clearly that the graph is that of the integrand in the expression for $E[X]$ and not "on the following picture ($t$-distribution with one df)" because the picture is neither of the $T$ distribution nor of the $t$ density with one df? Ditto for the second graph which shows $x^2f(x)$. Thanks. – Dilip Sarwate Jan 19 '12 at 23:08
-
The Holtsmark distribution ?
- 1,770
- 3
- 24
- 42
-
The variance of this distribution is infinite. The OP asked for distribution for which $\int x^2dF(x)$ does not exist in a sense that $\int_R sin(x)dx$ does not exist. Henry in its comment pointed out, that no such distribution exists. – mpiktas Dec 20 '11 at 15:00