5

I am a beginner in statistics.(and probability theory too).I studied Exponential distribution and just started doing problems when I got stuck in the following one:

Suppose that $X_1, . . . , X_n$ form a random sample of size $n$ from the exponential distribution with parameter $\beta$. Determine the distribution of the sample mean of $X_n$.

Can someone tell me how to approach the problem? Its a easy one( my intuition says) but unfortunately I am not being able to write down things step by step.

Qwerty
  • 1,047
  • 10
  • 22

2 Answers2

7

The sample mean is

$$ \bar{X}=\sum_{i=1}^{n}{\frac{x_i}{n}} $$

So, the r.v. $\bar{X}$ is the sum of the variables $y_i=x_i/n$. These variables have an exponential distribution with parameter $\beta/n$, and their sum is a gamma rv, with parameters $n$ and $\beta/n$.

This doesn't contradict the answer given by @Jon Egil, only that his answer is an aproximation that depends on the sample size, and this one is the exact distribution.

toneloy
  • 370
  • 1
  • 6
  • 2
    +1 Actually, your answer is not only correct but it _does_ contradict Jon Egil's answer, even though the OP has happily accepted Egil's answer. Indeed, as @Student001 pointed out, Egil's answer is not correct for _any_ finite $n$. – Dilip Sarwate Dec 13 '15 at 15:02
-1

Rephrased to better answer the original question, in line with the constructive comments.

The Central Limit Theorem (CLT), coined by George Pólya in 1920, is fundamental theorem for Probability Theory. Roughly, it states that the distribution of the sum (or average) of a large number of independent, identically distributed (iid) variables will approximate normal, regardless of the underlying distribution.

In relation to the point estimate of the mean, clearly, as more variables are sampled from the distribution, the sample mean is closer and closer to the underlying true mean. This is in accordance with the Weak Law of Large Numbers. Large is not defined clearly, but 30-50 is often cited as a reasonable number.

To build intuition, play with this R code and especially the sample size (50 below): 

 # Central Limit Theorem

r = 2 # rate for exponential distribution

set.seed(100) # To ensure reproducability

i <- 1000 # number of sample averages. 
          # We need multiple averages to draw a distribution of means
n <- 5    # number of draws from the distribution. This is the N in CLT

s <- rep(0, i)
for(i in 1:i){
  s[i] <- mean(rexp(n, rate=r))  # population size of 20 for
}

# Two plots vs normal distribution
par(mfrow=c(1,2))

qqnorm(s, main=paste("n=",n)); qqline(s, col="red") 

curve(dnorm(x, mean(s), sd(s)), from=0, to=1, ylim=c(min(density(s)$y),max(density(s)$y)))
lines(density(s), col='red')


# Shapiro-Wilks normality test
shapiro.test(s)

Please also see these two runs on my computer yielded the following results:

Firstly n=5 n=5

Secondly n=50 n=50

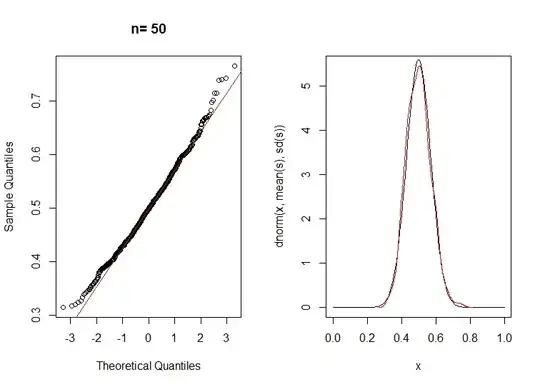
Visual inspection clearly shows the the bell curve of a normal distribution as n is large, while the small n has quite non-normal skew and tails.

Also note the Shapiro-Wilk normality test, available in R as: 

shapiro.test(s)

Running it for n=5 and n=50 will give much lower scores for n=5 than n=50, but in order to consistently reach p-values above 0.05, a much used cutoff, even n of 50 proved too low. 

n     p-value
5    < 2.2e-16
50   0.0008108
75   0.1061

Of these draws, only n=75 passed the Shapiro-Wilk normality test. Other seeds for the random generator will yield other results. But the general trend will remain, higher n means increasingly normal distribution of the sample mean.

A more formal discussion is available here.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
Jon Egil
  • 75
  • 5
  • That was a very very good one @Jon Egil . I am asking a further question, correct me if I am wrong.: The central limit theorem then implies that ,no matter what the distribution is, the sample mean will follow normal distribution as n tends to infinite: is this true? – Qwerty Dec 13 '15 at 12:47
  • 1
    Yes. As n becomes large even, and large very much is smaller than infinite. When pressed hard, my stats teacher said large was 30-50. I guess it varies by the underlying process, but even at 30-50 you'll start to see the pattern. – Jon Egil Dec 13 '15 at 13:21
  • 3
    Although an asymptotic-based approximation holds using the CLT, $\bar{X}_n$ will not be normal for any $n$, no matter how large. **EDIT** Maybe a (-1) was a bit harsh so I removed it. But I think the answer should point out that the sampling distribution is never normal. – ekvall Dec 13 '15 at 14:31
  • 1
    (-1) @JonEgil could you expand your answer..? We are looking for high-quality, self-contained answers rather than one-liners or link-only answers. How does CLT apply for this problem? – Tim Dec 13 '15 at 14:54
  • 2
    -1 I am downvoting this answer because it is just plain wrong, and even the addendum in a comment by Egil is misleading. The CLT is _not_ applicable to the question asked -- the WLLN is -- and the distribution of the sample mean converges (in probability) to a constant, not a normal distribution. – Dilip Sarwate Dec 13 '15 at 15:07
  • 1
    CLT is not about "$N$" samples (for any $N$), but about $N$ samples as $N \rightarrow \infty$ – Tim Dec 14 '15 at 14:55
  • 1 small doubt again. @Jon Egil . Int the R code you commented _# Two plots vs normal distribution ._ I thought it should display 3 graphs but it is displaying only two. Is your comment mis-written or the code for displaying curves? I used R studio for execution. – Qwerty Dec 14 '15 at 18:22
  • The line functions, qqline and line, just add a line to the previous plot. The comment is for both the qqplot and for the density plot. Hence two plots. – Jon Egil Dec 14 '15 at 21:06
  • You **still** have a completely incorrect statement in the second sentence of your answer. The CLT _does not_ say what you claim it says, roughly or otherwise. – Dilip Sarwate Dec 14 '15 at 21:32
  • For a practical counterexample to the 30-50 rule of thumb, see http://stats.stackexchange.com/questions/69898. For accounts of the CLT (and the additional conditions needed to address the objections by @Dilip) see http://stats.stackexchange.com/questions/3734 (for intuition) and http://stats.stackexchange.com/questions/81074, http://stats.stackexchange.com/questions/8884, and http://stats.stackexchange.com/questions/161804 (for more rigorous material). – whuber Dec 14 '15 at 21:40
  • @whuber My objections are perhaps better addressed in answers to the question [Central limit theorem versus law of large numbers](http://stats.stackexchange.com/q/22557/6633) which makes essentially the same incorrect statement as Egil does: "The central limit theorem states that the mean of i.i.d. variables, as N goes to infinity, becomes normally distributed." – Dilip Sarwate Dec 14 '15 at 22:02