Distribution of difference between two normal distributions

Question

I have two probability density functions of normal distributions:

$$f_1(x_1 \; | \; \mu_1, \sigma_1) = \frac{1}{\sigma_1\sqrt{2\pi} } \; e^{ -\frac{(x-\mu_1)^2}{2\sigma_1^2} }$$

and

$$f_2(x_2 \; | \; \mu_2, \sigma_2) = \frac{1}{\sigma_2\sqrt{2\pi} } \; e^{ -\frac{(x-\mu_2)^2}{2\sigma_2^2} }$$

I'm looking for the probability density function of the separation between $x_1$ and $x_2$. I think that means I'm looking for the probability density function of $|x_1 - x_2|$. Is that correct? How do I find that?

Answer 1

This question can be answered as stated only by assuming the two random variables $X_1$ and $X_2$ governed by these distributions are independent. This makes their difference $X = X_2-X_1$ Normal with mean $\mu = \mu_2-\mu_1$ and variance $\sigma^2=\sigma_1^2 + \sigma_2^2$. (The following solution can easily be generalized to any bivariate Normal distribution of $(X_1, X_2)$.) Thus the variable

$$Z = \frac{X-\mu}{\sigma} = \frac{X_2 - X_1 - (\mu_2 - \mu_1)}{\sqrt{\sigma_1^2 + \sigma_2^2}}$$

has a standard Normal distribution (that is, with zero mean and unit variance) and

$$X = \sigma \left(Z + \frac{\mu}{\sigma}\right).$$

The expression

$$|X_2 - X_1| = |X| = \sqrt{X^2} = \sigma\sqrt{\left(Z + \frac{\mu}{\sigma}\right)^2}$$

exhibits the absolute difference as a scaled version of the square root of a Non-central chi-squared distribution with one degree of freedom and noncentrality parameter $\lambda=(\mu/\sigma)^2$. A Non-central chi-squared distribution with these parameters has probability element

$$f(y)dy = \frac{\sqrt{y}}{\sqrt{2 \pi } } e^{\frac{1}{2} (-\lambda -y)} \cosh \left(\sqrt{\lambda y} \right) \frac{dy}{y},\ y \gt 0.$$

Writing $y=x^2$ for $x \gt 0$ establishes a one-to-one correspondence between $y$ and its square root, resulting in

$$f(y)dy = f(x^2) d(x^2) = \frac{\sqrt{x^2}}{\sqrt{2 \pi } } e^{\frac{1}{2} (-\lambda -x^2)} \cosh \left(\sqrt{\lambda x^2} \right) \frac{dx^2}{x^2}.$$

Simplifying this and then rescaling by $\sigma$ gives the desired density,

$$f_{|X|}(x) = \frac{1}{\sigma}\sqrt{\frac{2}{\pi}} \cosh\left(\frac{x\mu}{\sigma^2}\right) \exp\left(-\frac{x^2 + \mu^2}{2 \sigma^2}\right).$$

---

This result is supported by simulations, such as this histogram of 100,000 independent draws of $|X|=|X_2-X_1|$ (called "x" in the code) with parameters $\mu_1=-1, \mu_2=5, \sigma_1=4, \sigma_2=1$. On it is plotted the graph of $f_{|X|}$, which neatly coincides with the histogram values.

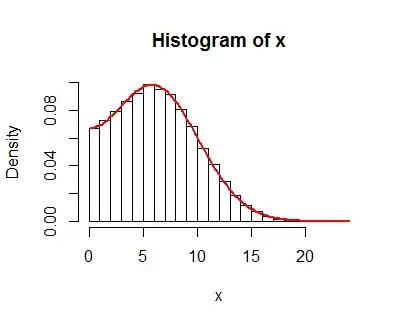
The R code for this simulation follows.

#
# Specify parameters
#
mu <- c(-1, 5)
sigma <- c(4, 1)
#
# Simulate data
#
n.sim <- 1e5
set.seed(17)
x.sim <- matrix(rnorm(n.sim*2, mu, sigma), nrow=2)
x <- abs(x.sim[2, ] - x.sim[1, ])
#
# Display the results
#
hist(x, freq=FALSE)
f <- function(x, mu, sigma) {
 sqrt(2 / pi) / sigma * cosh(x * mu / sigma^2) * exp(-(x^2 + mu^2)/(2*sigma^2)) 
}
curve(f(x, abs(diff(mu)), sqrt(sum(sigma^2))), lwd=2, col="Red", add=TRUE)

Answer 2

I am providing an answer that is complementary to the one by @whuber in the sense of being what a non-statistician (i.e. someone who does not know much about non-central chi-square distributions with one degree of freedom etc) might write, and that a neophyte could follow relatively easily.

Borrowing the assumption of independence as well as the notation from whuber's answer, $Z = X_1-X_2 \sim N(\mu, \sigma^2)$ where $\mu = \mu_1-\mu_2$ and $\sigma^2 = \sigma_1^2+\sigma_2^2$. Thus, for $x \geq 0$, \begin{align} F_{|Z|}(x) &\triangleq P\{|Z| \leq x\}\\ &= P\{-x \leq Z \leq x\}\\ &= P\{-x < Z \leq x\} &\scriptstyle{\text{since}~Z~\text{is a continuous random variable}}\\ &= F_Z(x) - F_Z(-x), \end{align} and of course, $F_{|Z|}(x) = 0$ for $x < 0$. It follows upon differentiating with respect to $x$ that \begin{align}f_{|Z|}(x) &\triangleq \frac{\partial}{\partial x} F_{|Z|}(x)\\ &= [f_Z(x) + f_Z(-x)]\mathbf 1_{(0,\infty)}(x)\\ &= \left[ \frac{\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)}{\sigma\sqrt{2\pi}} + \frac{\exp\left(-\frac{(x+\mu)^2}{2\sigma^2}\right)}{\sigma\sqrt{2\pi}}\right]\mathbf 1_{(0,\infty)}(x)\\ &= \frac{\displaystyle\exp\left(-\frac{x^2+\mu^2}{2\sigma^2}\right)}{\sigma\sqrt{2\pi}}\left(\exp\left(\frac{x\mu}{\sigma^2}\right) + \exp\left(\frac{-x\mu}{\sigma^2}\right)\right)\mathbf 1_{(0,\infty)}(x)\\ & = \frac{1}{\sigma}\sqrt{\frac{2}{\pi}} \cosh\left(\frac{x\mu}{\sigma^2}\right) \exp\left(-\frac{x^2 + \mu^2}{2 \sigma^2}\right)\mathbf 1_{(0,\infty)}(x) \end{align} which is the exact same result as in whuber's answer, but arrived at more transparently.

NOTE: Missing Neg Sign added to 2nd to Last Line - 2021/04/23

Answer 3

The distribution of a difference of two normally distributed variates X and Y is also a normal distribution, assuming X and Y are independent (thanks Mark for the comment). Here is a derivation: http://mathworld.wolfram.com/NormalDifferenceDistribution.html

Here you are asking the absolute difference, based on whuber's answer and if we assume the difference in mean of X and Y is zero, it's just a half normal distribution with two times the variance (thanks Dilip for the comment).