7

I have a regression problem and I am thinking of using ridge regression. One of the predictors is subject's gender, which is a categorical variable. How to take care of this variable for ridge regression modeling? Can it be encoded as $0$ and $1$? What to do with a categorical variable with more than $2$ categories?

amoeba
  • 93,463
  • 28
  • 275
  • 317
prashanth
  • 3,747
  • 4
  • 21
  • 33

2 Answers2

6

You are correct to assume that a categorical variable is encoded as indicator function/vector in your design matrix $X$; this is standard. To that respect, usually one of the levels is omitted and subsequently treated as baseline (if not you would have surely a rank-deficient design matrix when incorporating an intercept).

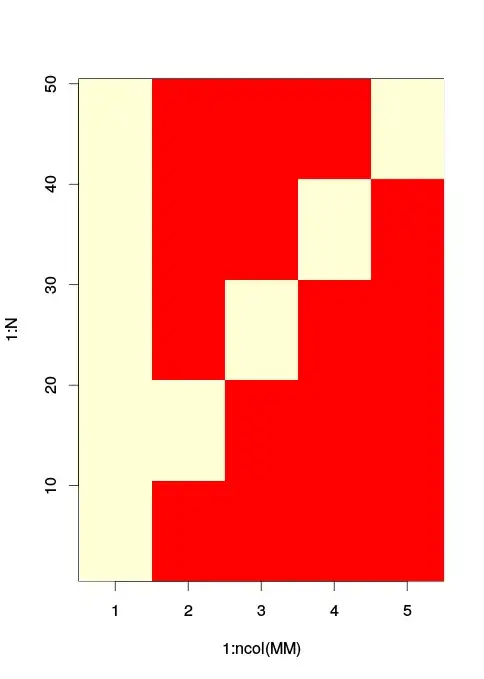
If you have a categorical variable with multiple categories you will once more treat is as an indicator function in your design matrix $X$. Just now you will not have a vector but a smaller submatrix. Lets see and example with R:

set.seed(123)
N = 50; # Sample size
x = rep(1:5, each = 10) # Make a discrete variable with five levels
b = 2
a = 3 # Intercept
epsilon = rnorm(N, sd = 0.1)

y = a + x*b + epsilon; # Your dependant variable

xCat = as.factor(x) # Define a new categorical variable based on 'a'

lm0 = lm(y ~ xCat)


MM = model.matrix(lm0) # The model matrix you use
image(x = 1:ncol(MM), y = 1:N, z=t(MM))  # The matrix image used. / Red is zero

Image of design matrix

As you see the levels 2,3,4 and 5 are encoded as separate indicator variables along the columns 2 to 5. The columns of ones in the column 1 is your intercept, level 1 is automatically omitted as an individual column and is assumed active alongside the intercept.

OK, so what about the ridge parameter $\lambda$? Remember that ridge regression is essentially using a Tikhonov regularized version of the covariance matrix of $X$. ie. $\hat{\beta} = (X^TX + \lambda I)^{-1} (X^T y)$, to generate the estimates $\hat{\beta}$. That is not problem for you if you have discrete (categorical) or continuous variables in your $X$ matrix. The regularization takes part outside the actual variable definition and essentially "amps" the variance across the diagonal of the matrix $X^TX$ (the matrix $X^TX$ can be thought of as a scaled version of covariance matrix when that the elements of $X$ are centred).

Please note that, as seanv507 and amoeba correctly comment, when using ridge regression it might make sense to standardise all the variables beforehand. If you fail to do that, the effect of regularisation can vary substantially. This is because increasing the observed variance of a particular variable $x$ by $\lambda$ can massively alter your intuition about $x$ depending on the original variance of $x$. This recent thread here shows such a case where regularization made a very observable difference.

usεr11852
  • 33,608
  • 2
  • 75
  • 117
  • 1
    Ridge regression depends on scale of input variables, so have to decide how you rescale your input variables.. Eg zero mean variance 1 for categorical variables too? It's not so clear (same as with ordinary variables... Depends on whether scale is meaningful relative to other variables) – seanv507 Dec 10 '15 at 12:06
  • Sorry, I cannot understand your comment fully. All regression algorithms depend on the scale of your variables. You can $z$-transform them but your need to be careful what you want to ultimately do. The thread [here](https://stats.stackexchange.com/questions/29781/when-conducting-multiple-regression-when-should-you-center-your-predictor-varia/29783#29783) elaborates on standardising your variables more. Clearly picking the parameter $\lambda$ is an issue in itself. – usεr11852 Dec 10 '15 at 12:12
  • 2
    I mean that linear regression is invariant [equivariant?]to a rescaling of the input variables ( the size of the coefficients changes, but the output doesn't change). But if you rescale the inputs for ridge regression you will get a different solution - because it is penalising the size of the coefficients (see eg bottom of page 63 Elements of statistical learning) – seanv507 Dec 10 '15 at 12:33
  • Yeah, sure; I agree. it would be nonsensical to use the same $\lambda$ with scaled and unscaled parameters. I never said one should do that; if anything I mentioned centring which affects only the intercept. – usεr11852 Dec 10 '15 at 12:54
  • 1
    that's not the point: consider eg a 'polynomial' linear regression ( ie you add $x^2,...x^n$), if your variables are not normalised with variance >1, then ridge regression will penalise the linear terms vs highest order terms ( which will have very small coefficients) - if you normalise, ridge regression does what you would like..ie prefer lower order polynomial. On other hand, lets say x and y are coordinates of something only moving in x direction but measurement noise adds a bit of variance to the y direction then ridge regression with unnormalised variables does what you want. – seanv507 Dec 10 '15 at 13:17
  • 3
    +1, but @seanv507 raises a good point (+1), which I would formulate as follows: if some of the predictors are continuous and some are binary, then the binary ones are likely to have very different variance from the continuous ones, and the ridge penalty will have very different effects on them. Hence, when using ridge regression it might make sense to standardize all variables, including the binary ones. – amoeba Dec 10 '15 at 14:35
  • @seanv507: Thank you for all your comments (and especially the later one, +1 to that too), I was initially uncertain about what you tried to draw attention on. Yes, you are right this is a valid point regarding ridge regression. I will add a sentence about it later today. – usεr11852 Dec 10 '15 at 18:02
  • @amoeba: Binary variables have a std. dev. between [0, 0.5] essentially, would I normalised them always? I don't know. I do not find it catastrophic, if the other vars have unit variance. in the end of the day it actually perplexes the interpretation of the related $\beta$ slightly, as there is not "standard unit" in the binary sense. (Thanks for clarifying what my sleepy self couldn't sort out! +1 :) ) – usεr11852 Dec 10 '15 at 18:08
  • Ok I standardize all variables in the training data. Does this transformation required for the test data as well. Since we can back transform the estimated coefficients to the original scale, transforming or standardizing the test data seems not necessary. Pls correct me if wrong. – prashanth Feb 08 '16 at 14:19
  • Yes, of course you need to standardize your test data as well. – usεr11852 Feb 08 '16 at 20:03
  • @usεr11852 If a categorical variable with k levels is encoded as k-1 binary variables. You say that the omitted variable is assumed active alongside the intercept. But this intercept is also active for all the variables in the model. I mean because its a constant it affect the entire model i guess. Suppose a new test observation is in the ommited level, how the model predicts for it. Please could you throw more light to this? – prashanth Feb 25 '16 at 06:29
  • If a new test observation is in the "omitted (reference) level" (level `1`) the model simply assumes that the all the other variables are inactive. When level `2` is active the $\beta$ coefficient is the effect of level `2` taking into account the effect of level `1`. – usεr11852 Feb 25 '16 at 08:55
1

Yes you can, your beta_ridge will be a number that will pop up when gender is 1 and won't have an effect when gender is 0. If you have more than one category, in my experience, make them all binary. e.g. if you have apple, orange, pear, instead of saying 1,2,3 say is_apple = [0,1] is_orange=[0,1] is_pear=[0,1].

maininformer
  • 451
  • 2
  • 8
  • Thanks. So you mean to say that instead of using a single variable, make it to three variables which are orange (0/1), apple (0/1) and pear (0/1) – prashanth Dec 10 '15 at 11:59
  • 1
    @user3761534 If you want you use all the levels of your `fruit` variable you will need to make sure you do not use an intercept. If you do have an intercept you will need to omit one of them. Otherwise your design matrix will be rank-deficient. This is why `sex` is usually a single indicator and "*pops up when gender is 1*'. – usεr11852 Dec 10 '15 at 12:08
  • @apt-getinstallhappyness yes exactly – maininformer Dec 10 '15 at 19:17
  • @usεr11852 Im not sure if identifiability is an issue when we have 1 equation and n>p, as opposed to a ,say, multinomial logit setting. If you could please provide a proof of that you would save me a lot of time :) . Another issue with using all the levels is that our betas will scale up and down based on the category value, in that pear might have a lower beta than apple even if their effects were equal. – maininformer Dec 10 '15 at 19:23
  • I do not comment on identifiability; I am talking abut rank-deficiency of your design matrix in the case you write out the full `fruit` variable and use an intercept. See the example in my answer. If you have "one equation" it means you already did what I describe, ie. you did not use all the available levels. – usεr11852 Dec 10 '15 at 19:47
  • Oh yeah. Agreed. – maininformer Dec 10 '15 at 21:04