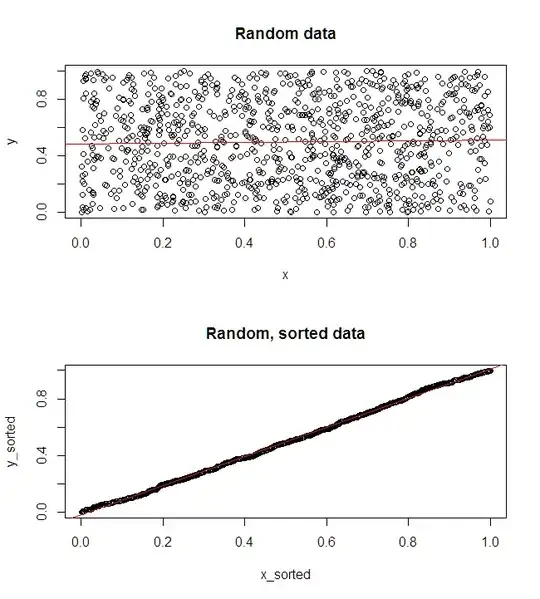
I'm not sure what your boss thinks "more predictive" means. Many people incorrectly believe that lower $p$-values mean a better / more predictive model. That is not necessarily true (this being a case in point). However, independently sorting both variables beforehand will guarantee a lower $p$-value. On the other hand, we can assess the predictive accuracy of a model by comparing its predictions to new data that were generated by the same process. I do that below in a simple example (coded with R).
options(digits=3) # for cleaner output
set.seed(9149) # this makes the example exactly reproducible
B1 = .3
N = 50 # 50 data
x = rnorm(N, mean=0, sd=1) # standard normal X
y = 0 + B1*x + rnorm(N, mean=0, sd=1) # cor(x, y) = .31
sx = sort(x) # sorted independently
sy = sort(y)
cor(x,y) # [1] 0.309
cor(sx,sy) # [1] 0.993
model.u = lm(y~x)
model.s = lm(sy~sx)
summary(model.u)$coefficients
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.021 0.139 0.151 0.881
# x 0.340 0.151 2.251 0.029 # significant
summary(model.s)$coefficients
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 0.162 0.0168 9.68 7.37e-13
# sx 1.094 0.0183 59.86 9.31e-47 # wildly significant
u.error = vector(length=N) # these will hold the output
s.error = vector(length=N)
for(i in 1:N){
new.x = rnorm(1, mean=0, sd=1) # data generated in exactly the same way
new.y = 0 + B1*x + rnorm(N, mean=0, sd=1)
pred.u = predict(model.u, newdata=data.frame(x=new.x))
pred.s = predict(model.s, newdata=data.frame(x=new.x))
u.error[i] = abs(pred.u-new.y) # these are the absolute values of
s.error[i] = abs(pred.s-new.y) # the predictive errors
}; rm(i, new.x, new.y, pred.u, pred.s)
u.s = u.error-s.error # negative values means the original
# yielded more accurate predictions
mean(u.error) # [1] 1.1
mean(s.error) # [1] 1.98
mean(u.s<0) # [1] 0.68
windows()
layout(matrix(1:4, nrow=2, byrow=TRUE))
plot(x, y, main="Original data")
abline(model.u, col="blue")
plot(sx, sy, main="Sorted data")
abline(model.s, col="red")
h.u = hist(u.error, breaks=10, plot=FALSE)
h.s = hist(s.error, breaks=9, plot=FALSE)
plot(h.u, xlim=c(0,5), ylim=c(0,11), main="Histogram of prediction errors",
xlab="Magnitude of prediction error", col=rgb(0,0,1,1/2))
plot(h.s, col=rgb(1,0,0,1/4), add=TRUE)
legend("topright", legend=c("original","sorted"), pch=15,
col=c(rgb(0,0,1,1/2),rgb(1,0,0,1/4)))
dotchart(u.s, color=ifelse(u.s<0, "blue", "red"), lcolor="white",
main="Difference between predictive errors")
abline(v=0, col="gray")
legend("topright", legend=c("u better", "s better"), pch=1, col=c("blue","red"))
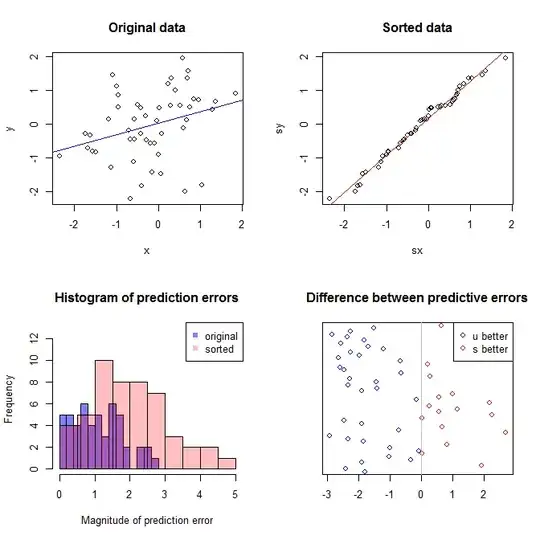
The upper left plot shows the original data. There is some relationship between $x$ and $y$ (viz., the correlation is about $.31$.) The upper right plot shows what the data look like after independently sorting both variables. You can easily see that the strength of the correlation has increased substantially (it is now about $.99$). However, in the lower plots, we see that the distribution of predictive errors is much closer to $0$ for the model trained on the original (unsorted) data. The mean absolute predictive error for the model that used the original data is $1.1$, whereas the mean absolute predictive error for the model trained on the sorted data is $1.98$—nearly twice as large. That means the sorted data model's predictions are much further from the correct values. The plot in the lower right quadrant is a dot plot. It displays the differences between the predictive error with the original data and with the sorted data. This lets you compare the two corresponding predictions for each new observation simulated. Blue dots to the left are times when the original data were closer to the new $y$-value, and red dots to the right are times when the sorted data yielded better predictions. There were more accurate predictions from the model trained on the original data $68\%$ of the time.
The degree to which sorting will cause these problems is a function of the linear relationship that exists in your data. If the correlation between $x$ and $y$ were $1.0$ already, sorting would have no effect and thus not be detrimental. On the other hand, if the correlation were $-1.0$, the sorting would completely reverse the relationship, making the model as inaccurate as possible. If the data were completely uncorrelated originally, the sorting would have an intermediate, but still quite large, deleterious effect on the resulting model's predictive accuracy. Since you mention that your data are typically correlated, I suspect that has provided some protection against the harms intrinsic to this procedure. Nonetheless, sorting first is definitely harmful. To explore these possibilities, we can simply re-run the above code with different values for B1 (using the same seed for reproducibility) and examine the output:
B1 = -5:
cor(x,y) # [1] -0.978
summary(model.u)$coefficients[2,4] # [1] 1.6e-34 # (i.e., the p-value)
summary(model.s)$coefficients[2,4] # [1] 1.82e-42
mean(u.error) # [1] 7.27
mean(s.error) # [1] 15.4
mean(u.s<0) # [1] 0.98
B1 = 0:
cor(x,y) # [1] 0.0385
summary(model.u)$coefficients[2,4] # [1] 0.791
summary(model.s)$coefficients[2,4] # [1] 4.42e-36
mean(u.error) # [1] 0.908
mean(s.error) # [1] 2.12
mean(u.s<0) # [1] 0.82
B1 = 5:
cor(x,y) # [1] 0.979
summary(model.u)$coefficients[2,4] # [1] 7.62e-35
summary(model.s)$coefficients[2,4] # [1] 3e-49
mean(u.error) # [1] 7.55
mean(s.error) # [1] 6.33
mean(u.s<0) # [1] 0.44