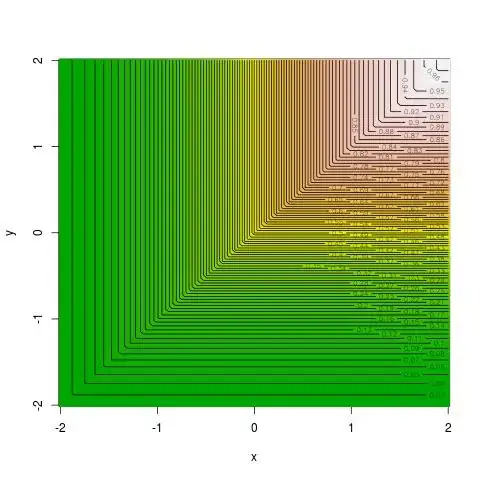
Is this a proper way to simulate the joint cdf of normal rvs with perfect positive correlation?
I followed these steps:
I generate 10 000 observations for two independent uniform rvs, $U_1\sim U(0,1),U_2\sim U(0,1)$.
The copula function for perfectly dependent rvs is the comonotonicity copula $C(u_1,u_2)=min(u_1,u_2)$. I plug in the simulated values of $U_1$ and $U_2$ to get simulated values of $C$.
I transform $U_1$ and $U_2$ using the std. normal quantile function, to get $X_1\equiv \Phi^{-1}(U_1)$, $X_2\equiv \Phi^{-1}(U_2)$.
I then gather together the simulated $(X_1,X_2,C)$. If I plot this triplet in a 3-dimensional plot, should it represent the cdf of bivariate normal variables with correlation coeff. 1?
Edit: This is not simulating from a Gaussian copula. This is about generating the cdf itself (the cdf depends on the marginal distributions).