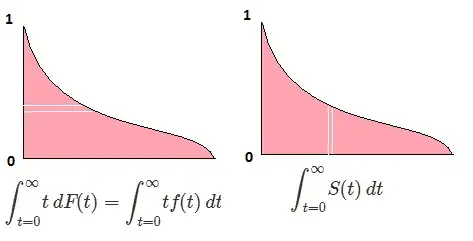
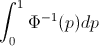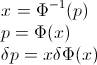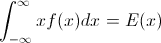Let $F$ be the CDF of the random variable $X$, so the inverse CDF can be written $F^{-1}$. In your integral make the substitution $p = F(x)$, $dp = F'(x)dx = f(x)dx$ to obtain
$$\int_0^1F^{-1}(p)dp = \int_{-\infty}^{\infty}x f(x) dx = \mathbb{E}_F[X].$$
This is valid for continuous distributions. Care must be taken for other distributions because an inverse CDF hasn't a unique definition.
Edit
When the variable is not continuous, it does not have a distribution that is absolutely continuous with respect to Lebesgue measure, requiring care in the definition of the inverse CDF and care in computing integrals. Consider, for instance, the case of a discrete distribution. By definition, this is one whose CDF $F$ is a step function with steps of size $\Pr_F(x)$ at each possible value $x$.
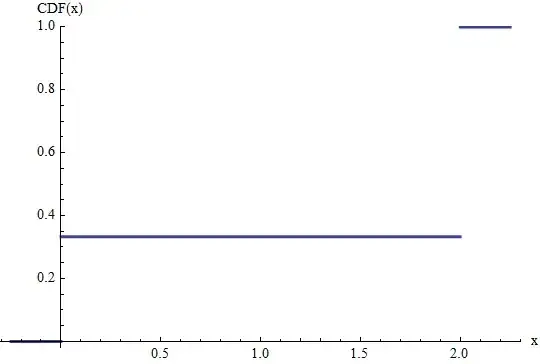
This figure shows the CDF of a Bernoulli$(2/3)$ distribution scaled by $2$. That is, the random variable has a probability $1/3$ of equalling $0$ and a probability of $2/3$ of equalling $2$. The heights of the jumps at $0$ and $2$ give their probabilities. The expectation of this variable evidently equals $0\times(1/3)+2\times(2/3)=4/3$.
We could define an "inverse CDF" $F^{-1}$ by requiring
$$F^{-1}(p) = x \text{ if } F(x) \ge p \text{ and } F(x^{-}) \lt p.$$
This means that $F^{-1}$ is also a step function. For any possible value $x$ of the random variable, $F^{-1}$ will attain the value $x$ over an interval of length $\Pr_F(x)$. Therefore its integral is obtained by summing the values $x\Pr_F(x)$, which is just the expectation.
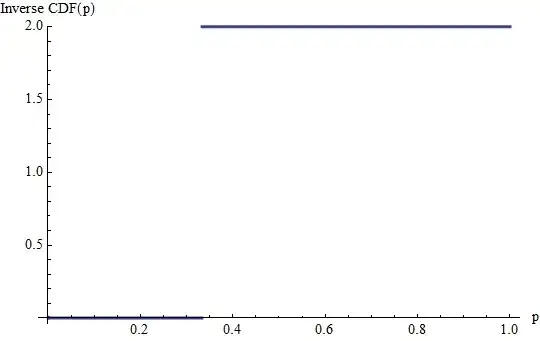
This is the graph of the inverse CDF of the preceding example. The jumps of $1/3$ and $2/3$ in the CDF become horizontal lines of these lengths at heights equal to $0$ and $2$, the values to whose probabilities they correspond. (The Inverse CDF is not defined beyond the interval $[0,1]$.) Its integral is the sum of two rectangles, one of height $0$ and base $1/3$, the other of height $2$ and base $2/3$, totaling $4/3$, as before.
In general, for a mixture of a continuous and a discrete distribution, we need to define the inverse CDF to parallel this construction: at each discrete jump of height $p$ we must form a horizontal line of length $p$ as given by the preceding formula.