I'm aware that this is a 'homework' question but it has gone unanswered for over six months so I figure the homework has been turned in by now. Also, the hints in the comments (which I use directly here) are useful until you get to the point where you have to calculate the expected value of the sample standard deviation (a non-trivial exercise), which I give a link to in this answer.
For a sample $X_1, X_2, ..., X_n$ from a $N(\mu,\sigma^2)$ population, the $95 \%$ confidence interval for $\mu$ when the variance $\sigma^2$ is unknown is
$$ \overline{X} \pm t_{n-1} \cdot \frac{s}{\sqrt{n}} $$
where $\overline{X} = \frac{1}{n} \sum_{i=1}^{n} X_i$ and $ s = \sqrt{ \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \overline{X})^2}$ and $t_{n-1}$ is the $97.5$th quantile of the $t$-distribution with $n-1$ degrees of freedom. From the expression for the confidence interval, we can see its width is the random variable $$W = 2t_{n-1} \cdot \frac{s}{\sqrt{n}}$$ The only random part of $W$ is $s$, therefore the expected width is
$ E(W) = \frac{2t_{n-1}}{\sqrt{n}} \cdot E(s) $, which reduces the problem to that of calculating $E(s)$ (which is calculated in this thread) and doing some algebra:
$$ E(W) = \sigma \cdot t_{n-1} \cdot \sqrt{ \frac{8}{n(n-1)} } \cdot \frac{ \Gamma(n/2) }{\Gamma( \frac{n-1}{2} ) } $$
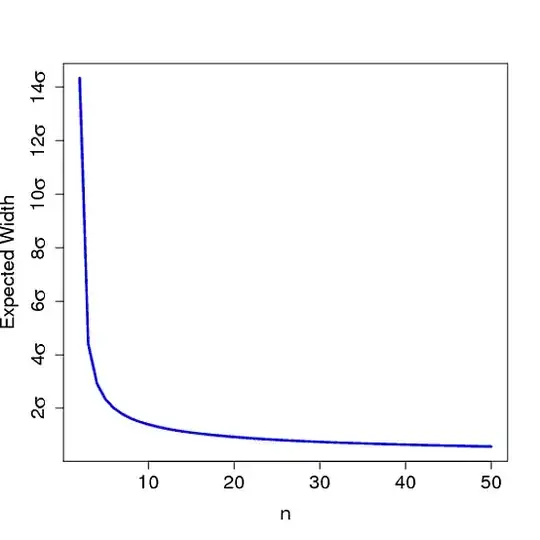
From that formula, we can plug in $n=9$ and find that $ E(W) \approx 1.49 \sigma $. We can also plot $E(W)$ as a function of $n$:
$\ \ \ \ \ \ \ \ \ $