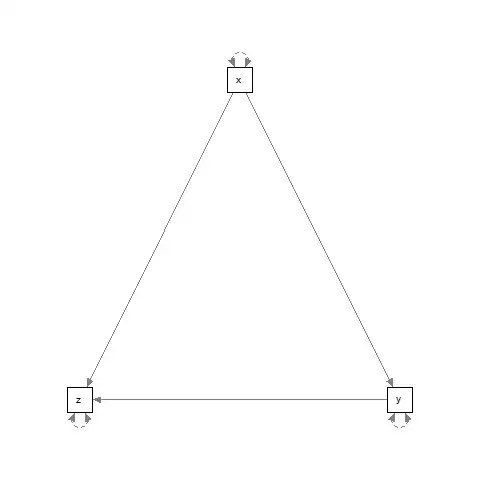
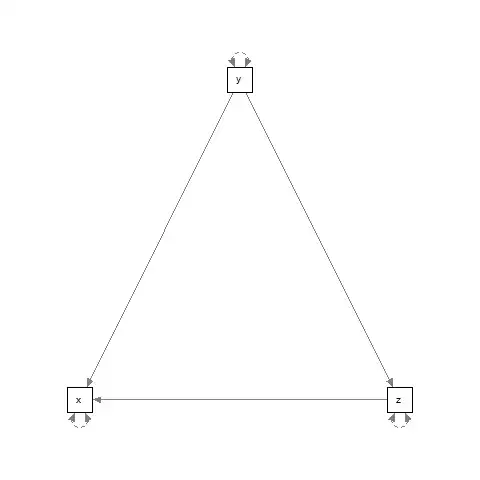
Suppose I have 3 manifest variables, x, y and z. I would like to use path analysis to determine the direction of influence. Is there a test that lets me distinguish between the following models?
and
In the first, z is caused directly by x, and indirectly by x through y. In the second, x is caused by y and z.
I fear that it is not, given that my SEM model is saturated in both cases, but I would like to be able to distinguish these situations.
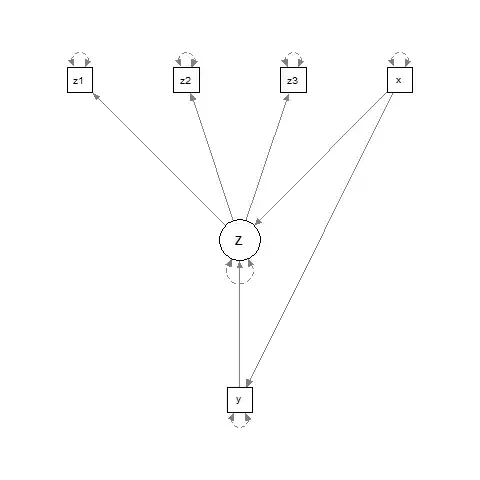
Would it make a difference if there were a measurement component to the model, as below?
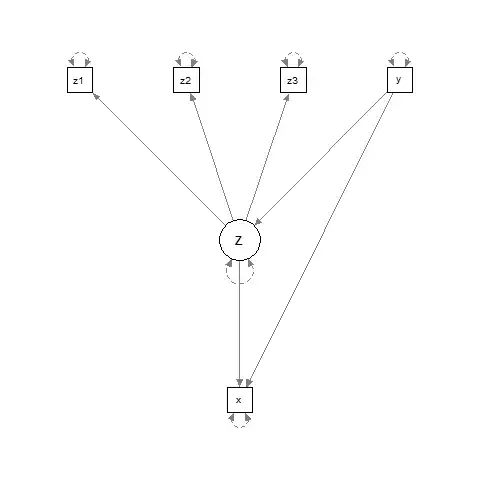
which should be distinguished from, say, this: