1

Let's say $Y$ is my DV, and $X_1$,and $X_2$ are IVs: \begin{align} \newcommand{\Cor}{\rm Cor} \Cor(Y,X_1) &= 0.7994172 \\ \Cor(Y,X_2) &= -0.00041 \\ \Cor(X_1,X_2) &= 0.505 \\[10pt] R^2_{Y|X_1X_2} &= 0.9315 \\ R^2_{Y|X_1} &= 0.624 \\ R^2_{Y|X_2} &= 0.00038 \end{align} Can any one explain this? I don't understand how this could happen.

gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
ChathuraG
  • 71
  • 6
  • 1
    You most likely have some form of an interaction between X1 and X2. What is the correlation between them? – Arun Jose Nov 18 '15 at 07:02
  • cor(X1,X2) = 0.5506106 – ChathuraG Nov 18 '15 at 14:30
  • The best example I can think of to give you an idea of how is: consider the problem of predicting how sweet a cup of tea would be if you were told two bits of information i) How many teaspoons of sugar was added ii) Was the cup of tea stirred?. Knowing only one of the two, probably only sugar would give you an idea of how sweet. Knowing if it was stirred would probably be a terrible predictor of sweetness. However, when you know how much sugar was added as well as if it was stirred you are bound to have a very high degree of confidence if the tea is going to be sweet! – Arun Jose Nov 18 '15 at 18:05

2 Answers2

1

You (almost certainly) have a suppressor variable. This can happen. The suppressor variable is correlated with (what you might consider) measurement error in the other variable. Including the suppressor allows the model to subtract out the measurement error and provide a clearer picture of the underlying dynamic. Suppressor variables are discussed in a few places on this site; a great place to start would be: Suppression effect in regression: definition and visual explanation/depiction.

A simple overview of the idea is that you are interested in the relationship between $X$ and $Y$, but you don't have access to $X$. Instead you have a variable $P$, which you can use as a proxy for $X$ in that it is caused by $X$ and $S$. In this case, including $S$ in the model will give you a clearer picture of the $X \rightarrow Y$ relationship.

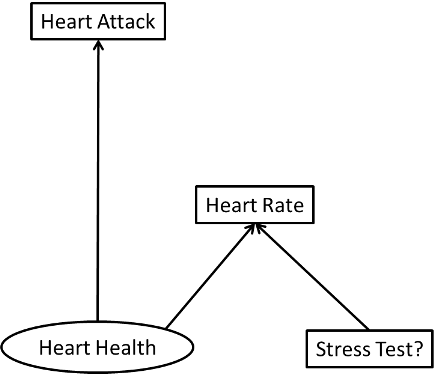
For the sake of greater clarity, consider this (contrived) example: You are interested in the effect of heart health on heart attacks. Unfortunately, you don't have a direct measure of heart health, but you do have heart rates for a set of patients. As it happens some of those heart rates were recorded while the patient was resting and some where recorded during a stress test (while the patient was briskly walking on a treadmill). Whether someone was walking on a treadmill once in the past is theoretically unrelated to the incidence of heart attacks, and it uncorrelated in your data. We can represent your situation with the following path diagram:

enter image description here

Here is a simple demonstration (coded in R): 

set.seed(9467)                              # this makes the example exactly reproducible
lo2p = function(lo){ exp(lo)/(1+exp(lo)) }  # we'll need this function to generate data

st = rep(c(0,1), each=30)                   # half were taking a stress test
hh = rnorm(60, mean=0, sd=3)                # heart health is normally distributed
hr = 75 + 1*hh + 70*st                      # heart rate is a function of hh & st
lo = -3 + 1*hh                              # these lines generate the output data
p  = lo2p(lo)
y  = rbinom(60, size=1, prob=p)

cor( y, st)  # [1] -0.1154701               # the stress test is uncorrelated w/ y
cor(hr, st)  # [1]  0.9942345               #  but highly correlaed w/ hr

summary(glm(y~hr+st, family=binomial))$coefficients         # st is highly significant &
#              Estimate Std. Error z value Pr(>|z|)         #  makes hr significant
# (Intercept) -110.7882    33.4078  -3.316 0.000912 ***
# hr             1.4413     0.4354   3.311 0.000931 ***
# st          -101.7561    30.6699  -3.318 0.000907 ***
summary(glm(y~hr,    family=binomial))$coefficients         # hr isn't significant alone
#                 Estimate  Std. Error    z value  Pr(>|z|)
# (Intercept) -0.800073314 0.977470881 -0.8185137 0.4130639
# hr          -0.002748774 0.008635833 -0.3182987 0.7502584
summary(glm(y~st,    family=binomial))$coefficients          # neither is st
#               Estimate Std. Error    z value   Pr(>|z|)
# (Intercept) -0.8472979  0.3984093 -2.1267018 0.03344487
# st          -0.5389965  0.6058574 -0.8896425 0.37365790
Community
  • 1
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
0

tl; dr: A low correlation does not mean that your variable is useless in the final model.

To answer your first question (can a multiple regression contain a IV that is not correlated with DV)

Yes, a multiple regression can contain an IV that is not correlated with the DV.

Assuming that you're only asking about linear regressions:

A multiple regression equation can and often will include independent variables that are not correlated at all with your dependent variable. In a simple regression (i.e. $Y$ ~ $X$) correlation is directly related to the R-squared, and so a low correlation pretty much means that a linear model will have a low R-squared. However, in multiple regression, there are a few situations where variables will have low correlations but still be useful in the model.

For your second question:

There's some sort of interaction between $X$1 and $X$2 which helps in understanding your Y. If you were to look at the regression coefficients in your linear model, there's a good chance that you'd find that both are statistically significant.

Kontorus
  • 427
  • 2
  • 10