I am checking that I have met the assumptions for multiple regression using the built in diagnostics within R. I think that from my online research, the DV violates the assumption of homoscedasticity (please see the residuals vs fitted plot below).
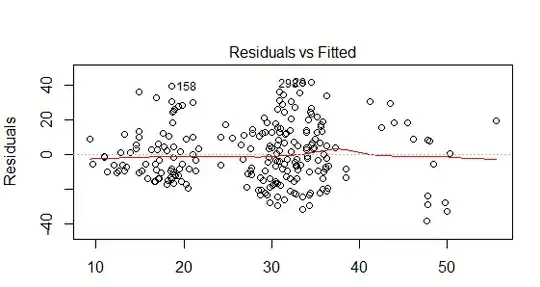
I tried log transforming the DV (log10) but this didn't seem to improve the residuals vs fitted plot. There are 2 dummy coded variables within my model and 1 continuous variable. The model only explains 23% of the variance in selection (DV) therefore, could the lack of homoscedasticity be because variable/s are missing? Any advice on where to go from here would be greatly appreciated.