Let $(X,Y)$ be uniformly distributed on the interior of the ellipse
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ where $a$ and $b$ are the
semi-axes of the ellipse. Then, $X$ and $Y$ have marginal densities
\begin{align}
f_X(x) &= \frac{2}{\pi a^2}\sqrt{a^2-x^2}\,\,\mathbf 1_{-a,a}(x),\\
f_X(x) &= \frac{2}{\pi b^2}\sqrt{b^2-y^2}\,\,\mathbf 1_{-b,b}(y),
\end{align}
and it is easy to see that $E[X] = E[Y] = 0$. Also,
\begin{align}
\sigma_X^2 = E[X^2] &= \frac{2}{\pi a^2}\int_a^a x^2\sqrt{a^2-x^2}\,\mathrm dx\\
&= \frac{4}{\pi a^2}\int_0^a x^2\sqrt{a^2-x^2}\,\mathrm dx\\
&= \frac{4}{\pi a^2}\times a^4 \frac 12\frac{\Gamma(3/2)\Gamma(3/2)}{\Gamma(3)}\\
&= \frac{a^2}{4},
\end{align}
and similarly, $\sigma_Y^2 = \frac{b^2}{4}$. Finally,
$X$ and $Y$ are uncorrelated random variables.
Let \begin{align}
U &= X\cos \theta - Y \sin \theta\\
V &= X\sin \theta + Y \cos \theta
\end{align}
which is a rotation transformation applied to $(X,Y)$. Then,
$(U,V)$ are uniformly distributed on the interior of an
ellipse whose axes do not coincide with the $u$ and $v$ axes.
But, it is easy to verify that $U$ and $V$ are zero-mean
random variables and that their variances are
\begin{align}
\sigma_U^2 &= \frac{a^2\cos^2\theta + b^2\sin^2\theta}{4}\\
\sigma_V^2 &= \frac{a^2\sin^2\theta + b^2\cos^2\theta}{4}
\end{align}
Furthermore,
$$\operatorname{cov}(U,V) = (\sigma_X^2-\sigma_Y^2)\sin\theta\cos\theta
= \frac{a^2-b^2}{8}\sin 2\theta$$
from which we can get the value of $\rho_{U,V}$.
Now, the ellipse on whose interior $(U,V)$ is uniformly distributed
has equation
$$\frac{(u \cos\theta + v\sin \theta)^2}{a^2}
+ \frac{(-u \sin\theta + v\cos \theta)^2}{b^2} = 1,$$
that is,
$$\left(\frac{\cos^2\theta}{a^2} + \frac{\sin^2\theta}{b^2}\right) u^2 + \left(\frac{\sin^2\theta}{a^2} + \frac{\cos^2\theta}{b^2}\right) v^2
+ \left(\left(\frac{1}{a^2} - \frac{1}{b^2}\right)\sin 2\theta \right)uv = 1,$$
which can also be expressed as
$$\sigma_V^2\cdot u^2 + \sigma_U^2\cdot v^2
-2\rho_{U,V}\sigma_U\sigma_V\cdot uv = \frac{a^2b^2}{4}\tag{1}$$
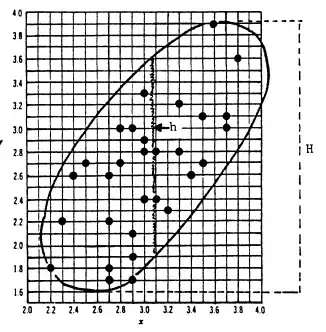
Setting $u = 0$ in $(1)$ gives
$\displaystyle h = \frac{ab}{\sigma_U}$.
while implicit differentiation of $(1)$ with respect to $u$ gives
$$\sigma_V^2\cdot 2u + \sigma_U^2\cdot 2v\frac{\mathrm dv}{\mathrm du}
-2\rho_{U,V}\sigma_U\sigma_V\cdot
\left(v + u\frac{\mathrm dv}{\mathrm du}\right) = 0,$$
that is, the tangent to the ellipse $(1)$ is horizontal at
the two points $(u,v)$ on the ellipse for which
$$\rho_{U,V}\sigma_U\cdot v = \sigma_v\cdot u.$$
The value of $H$ can be figured out from this, and will (in the
unlikely event that I have made no mistakes in doing the
above calculations) lead to the desired result.