17

Suppose that X, Y, and Z are random variables. X and Y are positively correlated and Y and Z are likewise positively correlated. Does it follow that X and Z must be positively correlated?

Pankaj Sharma
  • 885
  • 1
  • 8
  • 14
  • Your question is covered in numerous answers on site. See, for example, [here](http://stats.stackexchange.com/questions/122888/how-to-infer-correlations-from-correlations), or [here](http://stats.stackexchange.com/questions/5747/if-a-and-b-are-correlated-with-c-why-are-a-and-b-not-necessarily-correlated), or [a number of others](http://stats.stackexchange.com/search?q=correlation+bound) – Glen_b Nov 12 '15 at 06:51
  • 1
    But I didn't found any example to explain this answer. – Pankaj Sharma Nov 12 '15 at 06:57
  • The first link directly **shows** that the bounds on the correlation between X and Z can be negative (in the notation of that question, it shows that $\rho_{BC}$ is (attainably) bounded by $\rho_{AB}\rho_{AC}\pm {\sqrt{1-\rho_{AB}^2} \sqrt{1-\rho_{AC}^2}}$). e.g. take $\rho_{AB}=\rho_{AC}=0.5$ and the lower bound is negative. Aside from the need to substitute $A$ for $Y$ and so forth, how does that not directly answer your question? – Glen_b Nov 12 '15 at 07:05
  • It was not understandable to me – Pankaj Sharma Nov 12 '15 at 07:07
  • Then explain what you don't understand about it. Do you not understand what $\rho_{AB}$ means? (Or do you not understand what $\pm$ is? Or is it the $\sqrt{}$ symbol that's the problem?) I'll be happy to help clarify any part of the formula. – Glen_b Nov 12 '15 at 07:09
  • I have understood with explanation I provided so I posted it.. @Glen_b.. – Pankaj Sharma Nov 12 '15 at 07:29

2 Answers2

15

We may prove that if the correlations are sufficiently close to 1, then X and Z must be positively correlated.

Let’s assume C(x,y) is the correlation coefficient between x and y. Like wise we have C(x,z) and C(y,z). Here is an equation which comes from solving correlation equation mathematically :

C(x,y) = C(y,z) * C(z,x) - Square Root ( (1 - C(y,z)^2 ) * (1 - C(z,x)^2 ) )

Now if we want C(x,y) to be more than zero , we basically want the RHS of above equation to be positive. Hence, you need to solve for :

C(y,z) * C(z,x) > Square Root ( (1 - C(y,z)^2 ) * (1 - C(z,x)^2 ) )

We can actually solve the above equation for both C(y,z) > 0 and C(y,z) < 0 together by squaring both sides. This will finally give the result as C(x,y) is a non zero number if following equation holds true:

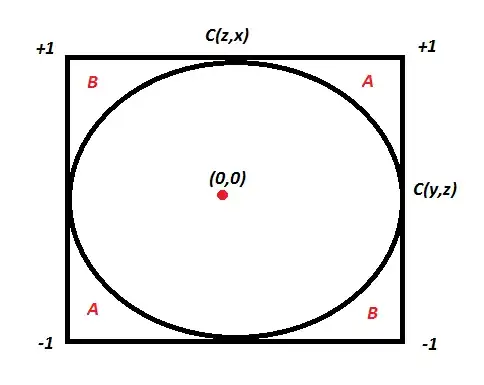
C(y,z) ^ 2 + C(z,x) ^ 2 > 1

Wow, this is an equation for a circle. Hence the following plot will explain everything :

correlation circle

If the two known correlation are in the A zone, the third correlation will be positive. If they lie in the B zone, the third correlation will be negative. Inside the circle, we cannot say anything about the relationship. A very interesting insight here is that even if C(y,z) and C(z,x) are 0.5, C(x,y) can actually also be negative.

Pankaj Sharma
  • 885
  • 1
  • 8
  • 14
5

Here is a great post by Terence Tao on the topic. Words from the man himself:

I came across the (important) point that correlation is not necessarily transitive: if $X$ correlates with $Y$, and $Y$ correlates with $Z$, then this does not imply that $X$ correlates with $Z$.

call-in-co
  • 838
  • 4
  • 15