2

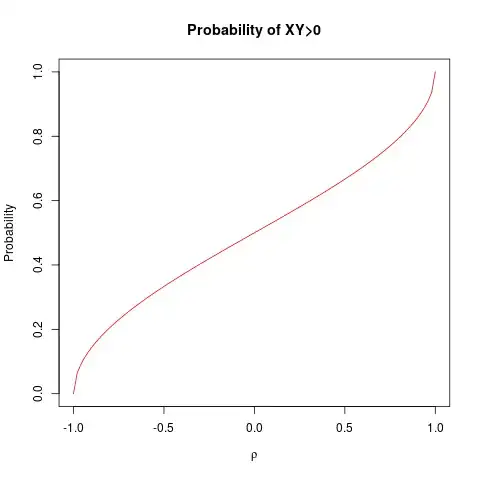
While doing questions related to Bi-variate Normal Distribution (BVN) I came across the following question which I was unable to decide how to proceed with:

If $(X,Y) \sim BVN(0,0,1,1;\rho )$ then prove that $P[XY > 0] = \frac{1}{2} + \frac{1}{\pi }{\sin ^{ - 1}}\rho $.

Is it possible to find the distribution of $XY$?

I was able to answer a similar question which asked to show that $P[X > 0,Y > 0] = \frac{1}{4} + \frac{1}{{2\pi }}{\sin ^{ - 1}}\rho $ where $(X,Y) \sim BVN(0,0,1,1;\rho )$

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
Kaustav Sen
  • 407
  • 3
  • 13
  • 1
    Yes, one can "find" the distribution of $XY$. Obtaining a closed analytical form for the CDF or PDF appears impossible: it involves integrating an error function, which can be done in closed form only for special values of $\rho$. – whuber Nov 10 '15 at 15:10
  • See also https://stats.stackexchange.com/questions/71260/what-is-the-intuition-behind-conditional-gaussian-distributions/71303#71303 – kjetil b halvorsen Jul 31 '17 at 14:30

2 Answers2

2

First, $\DeclareMathOperator{\P}{\mathbb{P}} \P(X Y > 0) = \P(X>0, Y>0 ~\text{or}~ X<0, Y<0)$ which is $2 \P(X>0,Y>0) ~~\text{(by symmetry)} $

Let us evaluate this by integrating a bivariate normal density. The density of $(X,Y)$ is given by $$ n(x,y) = \frac1{2\pi\sqrt{1-\rho^2}}\exp\left(-\frac1{2(1-\rho^2)}\cdot (x^2 + y^2 - 2\rho x y)\right) $$ So the sought-for probability is given by $$ \P(XY>0) = 2\int_0^\infty \int_0^\infty n(x,y) \; dx \; dy $$ That can be evaluated by first changing to polar coordinates with $dx\; dy = r \; dr \; d\theta$, integrating first with respect to $r$, which leaves (I leave out details) $$ \P(XY>0)= \frac1{\pi \sqrt{1-\rho^2}} \int_0^{\pi/2} \frac{1-\rho^2}{1-\rho\sin(2\theta)} \; d\theta $$ this one I evaluated by the help of maple, obtaining $$ \P(XY>0) = \frac12 + \frac1\pi \arctan(\frac{\rho}{\sqrt{1-\rho^2}}) $$ which is not the expression guessed (?) by the OP. But we can rewrite the answer above by using the identity $\arctan x = \arcsin(\frac{x}{\sqrt{x^2+1}})$ (see https://en.wikipedia.org/wiki/Inverse_trigonometric_functions), I leave that for the OP. Below a plot of this probability as a function of the correlation $\rho$:

enter image description here

It makes sense that the probability goes to zero when the correlation approaches $-1$, since then it becomes impossible that $X$ and $Y$ has the same sign.

kjetil b halvorsen
  • 63,378
  • 26
  • 142
  • 467
0

Let's decompose the event $XY > 0$ in events for $X$ and $Y$:

$\{XY > 0\} \Leftrightarrow \{X > 0 \;\; \& \;\; Y > 0\} \;\; | \;\; \{X < 0 \;\; \& \;\; Y < 0\}$

Also, you can prove:

$P[X > 0, \;\; Y > 0] = P[X < 0, \;\; Y < 0]$ (cf distribution of $(X, Y)$)

Thus, $P(XY > 0) = 2 * P[X > 0, \;\; Y > 0]$

tuomastik
  • 660
  • 6
  • 17
Raphaël Dubois
  • 16
  • 1