Pattern recognition: Not possible with linear classifiers for local and distributed information?

Question

I came across a paper with the following example to discuss the impossibility of localizing important features for certain patterns if linear classifiers are being used:

As I understand it, we have two classes at hand (pattern type 1 vs. pattern type 2), each class has data samples of different sorts (version 1 and version 2, could be for instance brain scans from different subjects - hence we have a certain variability in each class). Each feature can only take on two values (black or white in the illustration). As I understand it, it follows now that :

• Linear classifiers can can not distinguish between the two classes.

This is the case since a linear classifier calculates a weighted sum of all features - and despite the difference in patterns of class 1 and class 2, we always have the same number of inactive vs. active features - so the sums for each pattern type would not differ. Additionally I understand that no single feature drives the classifiers - since in each class each feature is both either active or inactive, depending on the pattern type. Hence we also do not have any useful local information. Hence as I see it, linear classifiers are only useful if single features are distinctive for class membership. If this is true though, what makes linear classifiers advantageous compared to say "classical" statistical univariate approaches?

An additional question would be how non-linear classifiers manage to make the distinction in the illustrated case - is it possible at all despite the variability in each class (pattern type)?

Thanks

Answer 1

In classification / pattern recognition we are trying to find f - the decision boundary between pattern type 1 and pattern type 2 (in the binomial case).

Let's go to the first question: * what makes linear classifiers advantageous compared to say "classical" statistical univariate approaches? * I assume by univariate, you mean you have one output variable.

Linear classifiers are always useful since they're relatively fast due to their simplicity. Take for example Perceptrons / Logistic Regression.

For logistic regression there is a closed form solution using the pseudo inverse / normal equation. See here (betas are w's I used here): https://en.wikipedia.org/wiki/Linear_least_squares_(mathematics)#The_general_problem Perceptrons are usually used when the learning is done online using stochastic gradient descent, which is not a closed form solution. Depending on your task one or the other might be more useful.

Either way, let's say you have some features. You can combine these features in a linear y = f1(x1 * w1 + x2 * w2 ... ) or whatever non-linear combination of features you want y = f2(x1 * x2 * w1 + x1^2 * w2 ... ) etc.

Now, linear means your decision boundary is a line. It's quite unlikely that in real world problems the classes are separable with a straight line. However, if you can manage to find a right representation (lets assume f2 above is) then you will be able to fit a straight line through the classes, however the feature space where you are doing that is different from the original space. In effect, in the above example I manually defined a different feature space. The model is still linear since I'm still fitting a line.

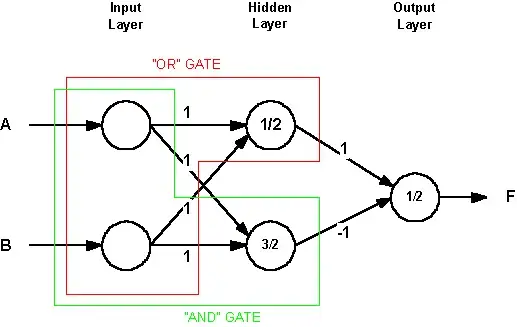
Here's a visual way of explaining it on finding the AND and XOR function.

This is a perceptron that can implement the AND function.

The general model is y1 = X0 * b + X1 * w11 + X2 * w12 where X0 = 1. (you add an extra degree of freedom which is always one, so your decision boundary isn't restricted at moving only through the origin). Then you find b, w11 and w12 and can learn the AND function, which is clearly linearly separable.

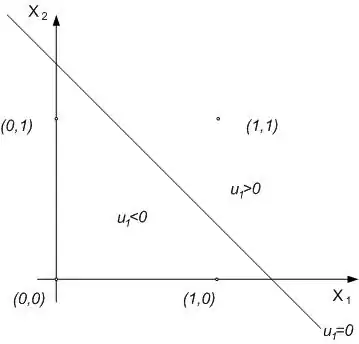
Now, let's say we want to find the XOR function.Here's how it looks like:

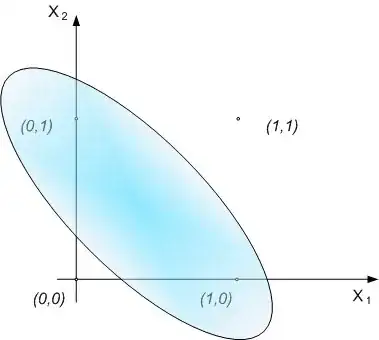
Well in the image above you can't divide the two classes with just one line. You can do it with one ellipse or with more than one line.

So, then you need to find a feature space where this decision boundary can be placed. Luckily, multi layer perceptrons can do that. In fact, this finds the feature space where you can put multiple such linear boundaries.

And I believe this also answers your second question as well.

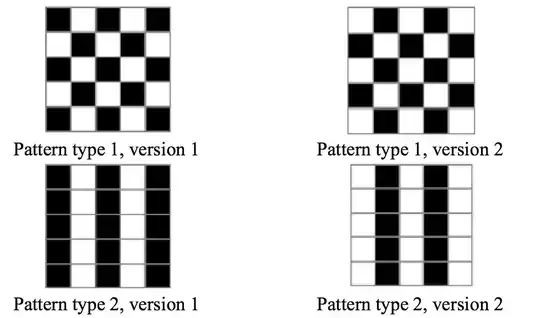
In effect, the right column images (version 2's) are the negation of your first images. That's invariant regardless of the class. So that's one feature, you can think about it as one perceptron / unit in the hidden layer. You wouldn't normally want to look at examples like this in the real world and find these invariances / rules manually, so u use multilayer perceptrons which do this for you automagically.

EDIT:

Okay, let's go at this manually over your example. You need at least two bits to be able to differentiate between the two patterns. I will take the first row and first feature from the second row. Then you can see that you only need the last feature from the first row and first feature from the second row.

P1 - V1: (0101)0 1 | V2 (1010)1 0

P2 - V1: (0101)0 0 | V2 (1010)1 1

So, 01 or 10 encodes pattern 1 while 00 or 11 encodes pattern 2. Now, these are original features from your data.

Now, let's look at the XOR function:

f1 f2 type (class)

0 1 1

1 0 1

0 0 0

1 1 0

A linear classifier is unable to learn the XOR function needed to classify these patterns.

For your example, it is impossible to classify the patterns using only one feature / predictor, regardless if you're using non-linear or linear classifiers.

Does that answer your question?