I am new to regression methods. I am creating Multiple Linear Regression, Partial Least Squares Regression and Principal Component Regression models for my dataset, and I am a bit confused with the results.
I have 60 predictors (or features) in my data, and 71 observations. Based on what I haver read (and understood), PLSR should give the best results. PCR should give results that are close to PLSR, and MLR is the most simplistic and which should give the worst results. Is my conclusion correct?
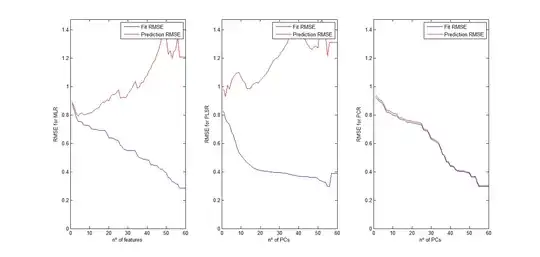
Because in my dataset, MLR and PLSR work very very similarly whereas PCR gives a much better prediction result. I have done a comparison of the methods, watching how the RMSE of the cross-validated methods changes with the number of features introduced for the MLR and PLSR methods, and with the number of PCs used for the PCR method. While MLR and PLSR suffer from overfitting very early, PCR keeps improving its prediction accuracy while the number of PCs is increased.
What do you think about this? Can this have a logical explanation?
This is what I am doing to compute PCR fit and prediction errors (Matlab code):
PCALoadings_all=PCALoadings;
PCAScores_all=PCAScores;
for ik=1:length(PCAVar) %add PCs one by one
PCALoadings=PCALoadings_all(:,1:ik);
PCAScores= PCAScores_all(:,1:ik);
%Function 'regress' needs a constant column so add it
PCAScores = [PCAScores, ones(length(PCAScores(:,1)),1)];
[betaPCR,~,~,~,statsPCR] = regress(labels-mean(labels), PCAScores); %Create regression model
betaPCR=betaPCR(1:end-1,:); %remove constant effect
size_PCR= find(betaPCR~=0, 1, 'last'); %find 0-value coefficients
%To make the PCR results easier to interpret in terms of the original
%spectral data, transform to regression coefficients for the original, uncentered variables.
betaPCR = PCALoadings*betaPCR;
%Create model
betaPCR_fit = [mean(labels) - mean(norm_feature_matrix)*betaPCR; betaPCR];
yfitPCR = [ones(d1,1) norm_feature_matrix]*betaPCR_fit; %compute fitted labels
%Cross-validate
predictMat=[];
for test_idx=1:length(labels)
testix = test_idx; %One value to test
trainix = setdiff(1:length(labels),testix); %All the other values to train
%Feature matrix and labels to train
X=norm_feature_matrix(trainix,:);
y=labels(trainix);
%Feature matrix and labels to test
X_test=norm_feature_matrix(testix,:);
y_test=labels(testix);
%compute beta with training data
betaPCR_CV = [mean(y) - mean(X)*betaPCR; betaPCR];
%prediction with test data
yCV_PCR = [1 X_test]*betaPCR_CV;
predictrow = [y_test, yCV_PCR]; % actual vs predicted
predictMat = [predictMat; predictrow];
end
RMSE_fit_PCR(ik) = sqrt(mean((yfitPCR - labels).^2)); %Compute RMSE for regression fit
RMSE_prediction_PCR(ik) = sqrt(mean((predictMat(:,1) - predictMat(:,2)).^2)); %Compute RMSE for prediction
%plot regressions
end
Do you think I'm doing something wrong? Did I misunderstood something?